
This page shows some results computed with the Hot Plate applet.
For particle radius 10–2 and 10–3, the displacement at t=100 reaches a peak at around 250 particles. For particle radius 10–4, the results are too noisy to be useful.



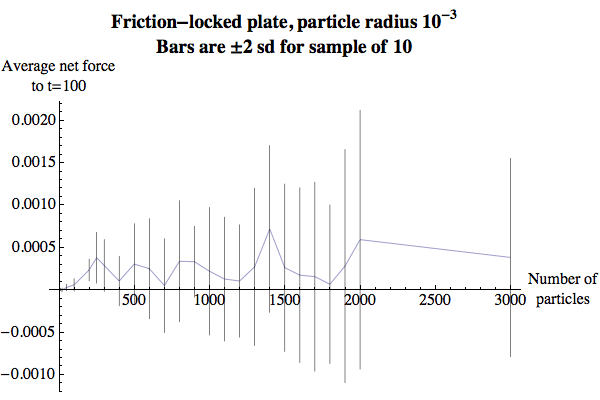
If the plate is locked by friction, the average net force on it is the net momentum delivered by particle collisions, divided by the time interval. (The advantage of locking the plate is that we see a persistent net force; when the plate is allowed to move, the momentum delivered by particle collisions includes drag forces, which over time bring the average net force to zero.) The results are much noisier and flatter than the displacements for the plate when it’s free to move; this suggests that the way the displacement curves forms a relatively sharp peak owes a lot to the increasing drag experienced by the plate as the number of particles increases.
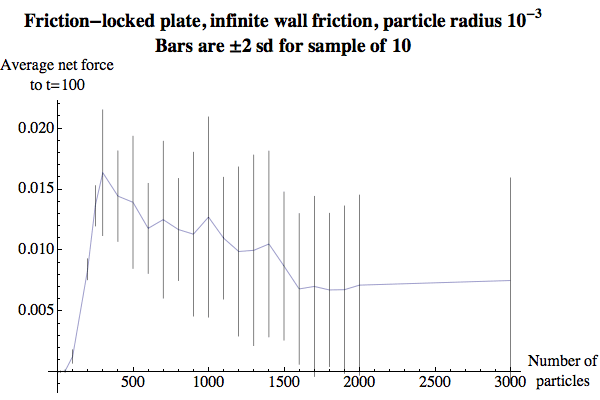
If we change the boundary conditions so there’s infinite friction between the particles and the container wall (i.e. the tangential velocity of any particle colliding with the wall is completely eliminated), the force on the plate is significantly enhanced; presumably this is because the frictional force that the wall is applying to the particles is ultimately being transferred by the particles to the plate.


|
|
|