Pick two points, P and Q, at random from the interior of a square. What is the probability that the line that passes through P and Q will intersect two opposite sides of the square, as opposed to two sides that are adjacent to each other?
I heard about this fun puzzle from Christopher Long. This page will describe a simple, geometrically intuitive solution, and then give a systematic way to solve generalisations to other shapes, and higher dimensions.
[Fine print: the points are picked uniformly at random, which means that the probability that each of them lies in any given region within the square is proportional to the area of that region, and independently, which means the probability for Q being in some region is completely unaffected by the position of P, and vice versa.]

For the sake of concreteness, assume the square has both x and y coordinates ranging from 0 to 1. Of course it will make no difference to the answer if the square has a different size, location, or orientation. We will call the coordinates of the two points (x1, y1) and (x2, y2).
Like many geometric probability puzzles, what we are seeking is the ratio between two areas or higher-dimensional volumes in some space: the volume of the region that describes all the possible outcomes under consideration, and the volume of the subset of that region that describes the particular outcome whose probability we wish to compute.
In this case, all the outcomes from choosing two different points within a square of side 1 can be described by a single point in a 4-dimensional hypercube, or 4-cube, of side 1, whose four coordinates, (x1, y1, x2, y2), give us the coordinates within the square of both points. The volume of this 4-cube is 1. So our problem is to find the volume of the subset of the 4-cube describing only those outcomes where the line through the two points intersects a pair of opposite sides of the square: either the top and bottom sides, or the left and right sides.
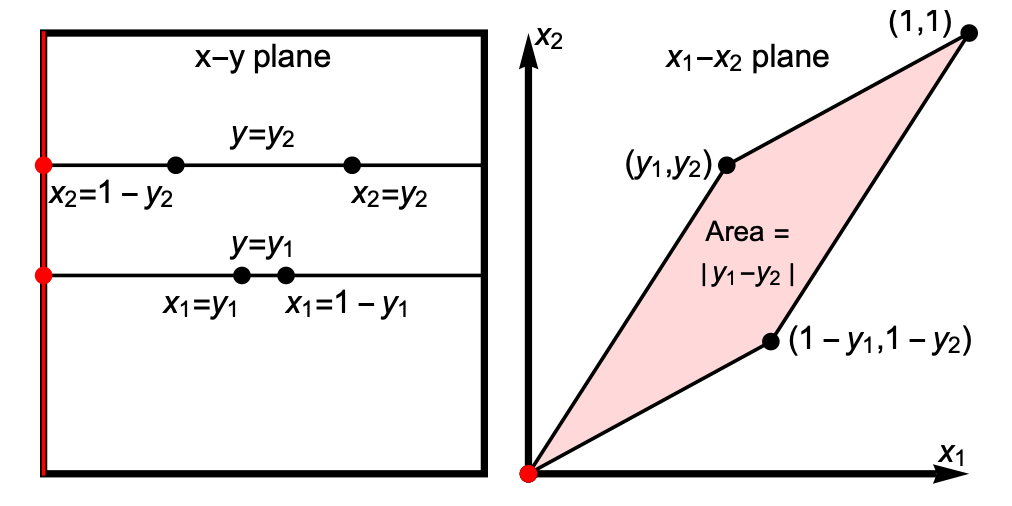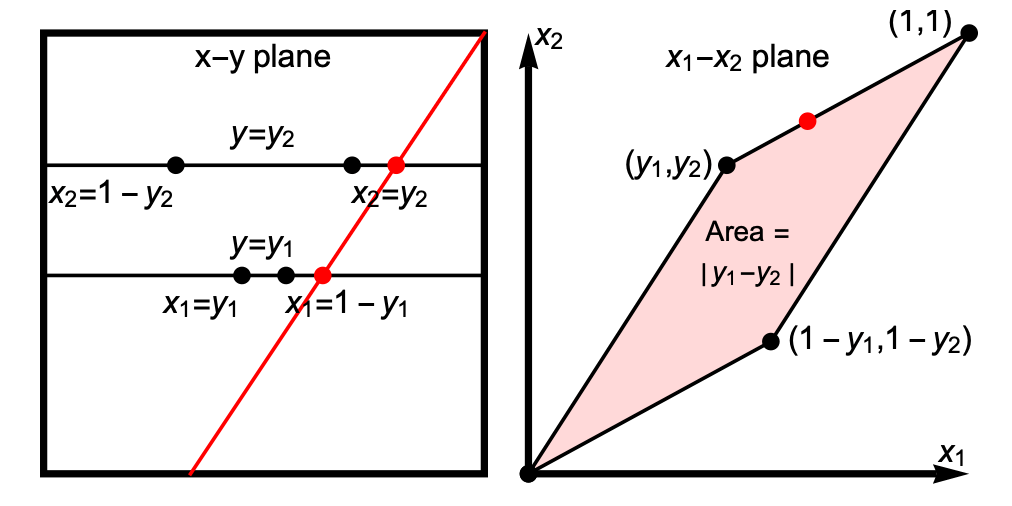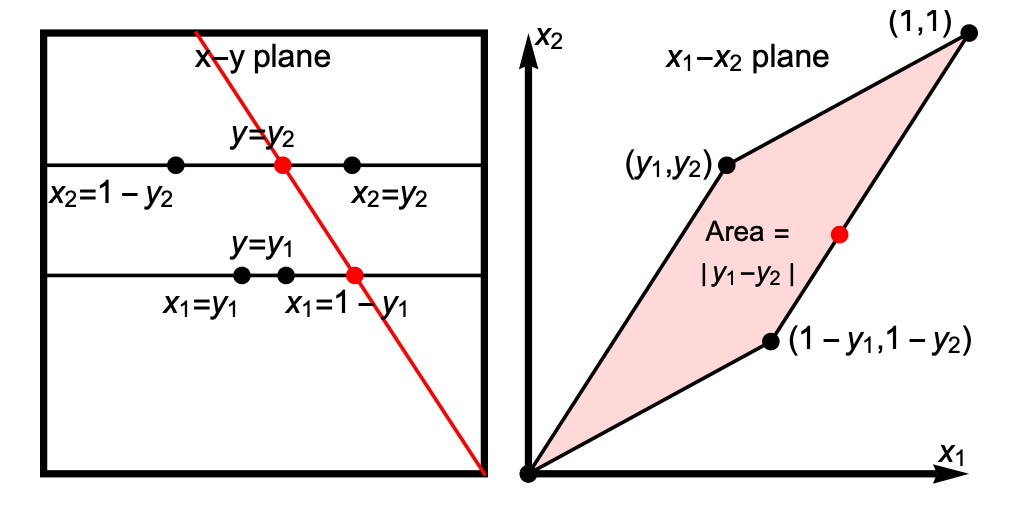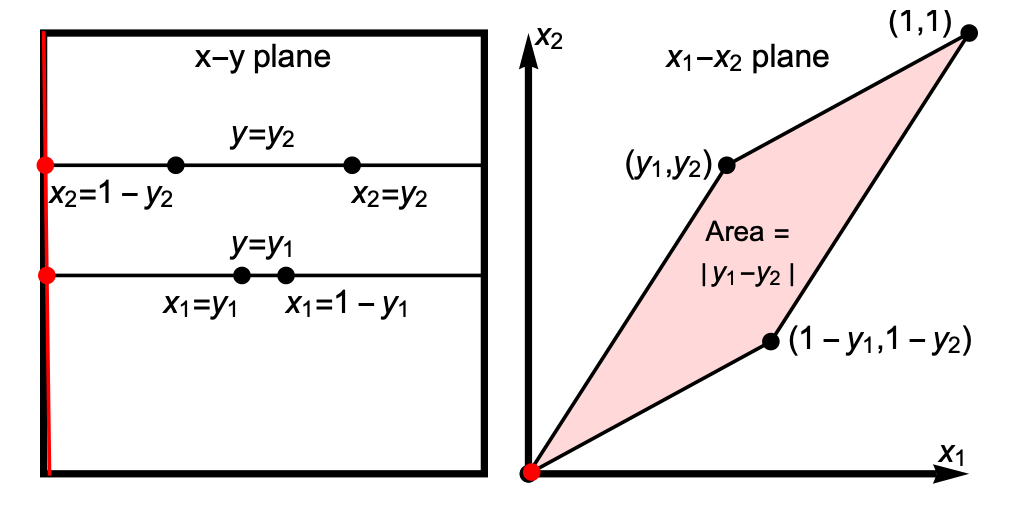
Imagine sweeping a line across the square (the red line in the first panel of the animation) so that it always joins the top and bottom sides, and one endpoint or the other is always in one of the corners of the square. These configurations for the line mark out the boundary of the region we are interested in. But what does this say about the two points that give us the line?
Suppose we hold y1 and y2 fixed for the moment, and compute the values of x1 and x2 such that both points lie on the red line. If we look at the result of this in the (x1, x2) plane (the red dot in the second panel of the animation), the point here sweeps out a parallelogram with vertices at (0,0), (y1,y2), (1,1) and (1–y1,1–y2).
The area of this parallelogram is simply:
|y1–y2|
So for any fixed y1 and y2, this is the probability that the line between the two points with uniformly random x1 and x2 joins the top and bottom edges of the square.
What is the average of |y1–y2| across all values of y1 and y2? This is just the volume of two pyramids with equal-sized triangular bases, one with y1 ≤ y2 and one with y1 ≥ y2. The height of both pyramids is 1, since that is the maximum that |y1–y2| reaches in both triangles. So the volume of each pyramid is 1/6, for a total of 1/3.
We multiply by two to account for the other case, where the pair of opposite edges are the left and right edges. So:
The probability that the line that passes through two randomly chosen points in a square intersects two opposite sides of the square is 2/3.
This result also tells us that the probability for the line passing through the points to intersect any two adjacent sides of the square is 1 – 2/3 = 1/3, which is the same as the probability for the line to intersect one of the specific pairs of opposite sides.
It turns out that we can construct a 4-volume-preserving 1-to-1 map between pairs of points whose line intersects any two adjacent sides, and pairs of points whose line intersects the left and right sides. This gives us another way of proving the result, without the need to perform any integration.
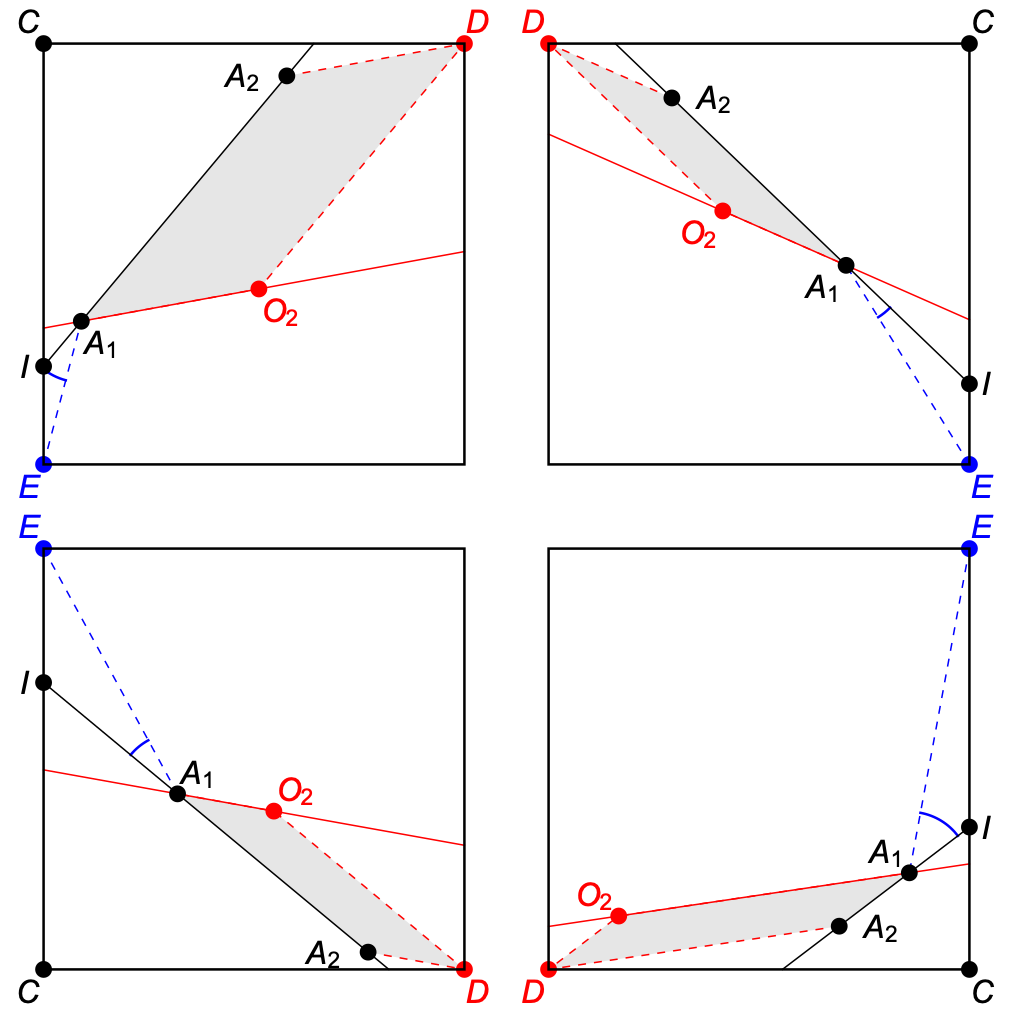
We will call the two points A1 and A2, and suppose the line containing them intersects two adjacent edges of the square that meet at the corner C. Let D be the other corner of the square at the same height. We will number our two points so the one closest to the line CD is the second one, A2. The diagram on the left shows examples for all four possibilities for C.
We can construct a parallelogram with A1, A2 and D as three of its vertices. If we require the parallelogram to stay inside the square, this means the fourth vertex must be:
O2 = D + (A1 – A2)
It is not hard to see that the line containing the pair of points A1 and O2 will always intersect the left and right sides of the square. On the A1 end, it must intersect the square between C and I, the point where the original line through A1 and A2 intersects the square. On the O2 end, it must intersect the square without crossing the line O2D, which means it cannot intersect CD, and since it slopes towards D as it approaches, it cannot hit the other horizontal side of the square either.
Note that for each choice of D, the map:
(A1, A2) → (A1, D + (A1 – A2))
is its own inverse, i.e. if we apply it twice we get back the original input. Because it is an affine map (a linear transformation plus a translation) it can only change 4-volumes by some constant factor, and since applying the map twice gives the identity map, the square of that factor must be 1, and the factor itself must be ±1. So the map preserves 4-volumes.
To see why the overall map is 1-to-1, given that the four individual maps are invertible, the only real issue is how we identify the correct D when all we have are the two points A1 and O2.
Examining the four cases, we can see that when the red line through A1 and O2 slopes upwards from left to right, the only two candidates for D are the top-right and bottom-left corners. We can choose the correct one by noting that it will always lie at the clockwise end of an arc (of less than 90 degrees) joining two lines pointing in the directions of A1E and DO2. In the diagram, where we have the line A1I shown, parallel to DO2, that makes a convenient place to perform the comparison with A1E and see what characterises the correct choice.
When the line through A1 and O2 slopes downwards from left to right, the only two candidates for D are the top-left and bottom-right corners, and the correct choice comes from the line at the counter-clockwise end of the arc.
Finally, we should note that so far we have been glossing over the difference between ordered and unordered pairs of points. If we insist that the point closest to CD is the “second” one, A2, then how should we handle ordered pairs of points where this isn’t true? The easiest way to resolve this is to assume we are dealing with unordered pairs, where we can name each point however we like. The total 4-volume of all unordered pairs of points is 1/2 rather than 1, but since all our subsets are halved in volume as well, and all that matters are the ratios, we end up with exactly the same probabilities.
We could also deal with ordered pairs and treat the two cases for the position of A1 and A2 with respect to CD separately. But however we handle this, our map shows that the 4-volume of the set of pairs of points whose lines intersect adjacent edges of the square is exactly half the 4-volume of the set whose lines intersect opposite edges.
Next, we will generalise this by looking at the situation where the space in which we choose the two points has an arbitrary dimension d ≥ 2, and in place of the two opposite edges of a square, we will ask if the line through the two chosen points intersects two parallel faces of a polytope, the generalisation of a 2-dimensional polygon or 3-dimensional polyhedron to any number of dimensions.
We will choose coordinates (x1, x2, ..., xd) for Rd in which the last coordinate, xd, of all the points of one of the faces is equal to zero, while for the other face it is some constant, h, which measures the orthogonal separation between the faces. We will use d–1 coordinates u = (u1, u2, ..., ud–1) to specify a point on the first face, and another d–1 coordinates v = (v1, v2, ..., vd–1) to specify a point on the second face. Apart from being flat, we will not assume anything about the shapes of these faces. The values of these u and v coordinates will be subject to certain restrictions that will determine the shapes in detail, but all we will need to know is the total (d–1)-volume of each face: the length for a 1-dimensional edge of a polygon, the area for a 2-dimensional face of a polyhedron, the volume for a 3-dimensional cell of a 4-dimensional polytope, etc.
Now, consider a line segment whose two endpoints on the two faces are given by:
F1(u) = (u1, u2, ..., ud–1, 0)
F2(v) = (v1, v2, ..., vd–1, h)
We can pick out two arbitrary points on that line segment with two more coordinates, λ and μ, which range from 0 to 1:
P1(u, v, λ, μ) = (1–λ) F1(u) + λ F2(v)
P2(u, v, λ, μ) = (1–μ) F1(u) + μ F2(v)
The point in the (2d)-dimensional space that contains all possible choices of both points is simply the result of glomming these two d-dimensional vectors together, which we will write as:
P1,2(u, v, λ, μ) = ((1–λ) F1(u) + λ F2(v), (1–μ) F1(u) + μ F2(v))
To compute the (2d)-volume of the region where our two chosen points, P1 and P2, lie on a line that intersects both faces, we will need to compute the Jacobian determinant of the function P1,2 with respect to the 2d parameters (u1, u2, ..., ud–1, v1, v2, ..., vd–1, λ, μ). This determinant tells us (up to a sign) the volume of an infinitesimal parallelepiped that is swept out in the (2d)-dimensional space of pairs of points in Rd if we vary the parameters within some infinitesimal cube. By integrating the absolute value of the Jacobian determinant across the full range of the parameters we get the (2d)-volume of the region we are trying to measure.
The Jacobian matrix J, the (2d)×(2d) matrix of partial derivatives of P1,2 with respect to the parameters, is:
| J | = |
|
The four blocks here where there are entries of 1–λ, 1–μ, λ and μ along the diagonals and zeroes elsewhere are of size (d–1)×(d–1).
Swapping rows or columns in a matrix preserves the absolute value of the determinant, so we can rearrange this matrix into another one whose determinant is a bit easier to compute:
| J* | = |
|
This new matrix, J*, is almost a block-diagonal matrix, with the only thing spoiling that being the vi–ui entries in the bottom two rows. However, we can see that these entries will have no effect on the determinant of J*. The determinant is a sum of products where each product includes entries from every row and every column of the matrix, and since the only non-zero entry in the last column of the matrix is the h in the last row, no other entry from the last row can avoid being multiplied by one of the zeroes from the last column. The same applies to the second-last column and the second-last row. So we can evaluate the determinant of J* as if those vi–ui entries were all zero, making its determinant the product of the determinants of all the 2×2 blocks along its diagonal.
|det(J)|
= |det(J*)|
= |(1–λ) μ – (1–μ) λ|d–1 h2
= |μ – λ|d–1 h2
We then integrate this across the allowed range for all the parameters. Since the u and v coordinates do not appear in the determinant at all, integrating over their allowed values just yields the (d–1)-dimensional areas of each face, which we will call A1 and A2.
Vol2d(A1, A2, h, d)
= ∫u ∫v ∫01 ∫01 |det(J)| dλ dμ dv du
= A1 A2 h2 ∫01 ∫01 |μ – λ|d–1 dλ dμ
= 2 A1 A2 h2 ∫01 ∫0μ (μ – λ)d–1 dλ dμ
= 2 A1 A2 h2 ∫01 (μd / d) dμ
= 2 A1 A2 h2 / [d (d+1)]
If the two faces we are considering belong to a convex regular polytope with f congruent faces of area A, then A1 = A2 = A, and the volume of the polytope itself is just f times the volume of a d-dimensional pyramid with base A and height h/2 (since h is the total distance between two opposite faces):
Volpoly(A, h, f, d) = f A h / (2d)
We then have the probability for the line containing two chosen points within the polytope intersecting both faces of some specific pair of opposite faces:
Probopp, 1(f, d)
= Vol2d(A, A, h, d) / Volpoly(A, h, f, d)2
= 8 d / [(d+1) f 2]
The formula we found for Vol2d can be applied to any convex polyhedron whose faces come in parallel pairs, but the independence of the probability Probopp, 1 from the detailed geometry of the polyhedron relies on the total volume of the polyhedron being a multiple of that for a single pyramid. This will not be true for the Archimedean polyhedra, which have faces with different shapes. However, it is true for rectangles, parallelograms, and all d-dimensional parallelepipeds, where the pyramids assocated with each face have different bases and heights, but the product of the two, and hence the pyramid’s volume, is the same for all faces.
The probability that the line intersects any of the pairs of opposite faces is then found by multiplying by f/2.
For a convex regular polytope or a parallelepiped in d dimensions, with f faces that come in opposite pairs, the probability that the line that passes through two randomly chosen points in the polytope will intersect any of the pairs of opposite faces is:
Probopp, any(f, d) = 4 d / [(d+1) f ]
We then have the following specific cases:
| Probability that the line that passes through two random points in a polytope intersects any of the pairs of opposite faces | |||
|---|---|---|---|
| Polytope | Dimension d | Number of faces f | Probability 4 d / [(d+1) f ] |
| Square, rectangle, parallelogram | 2 | 4 | 2/3 |
| Regular n-gon, even n | 2 | n | 8 / (3n) |
| Cube, rectangular prism, parallelepiped | 3 | 6 | 1/2 |
| Octahedron | 3 | 8 | 3/8 |
| Dodecahedron | 3 | 12 | 1/4 |
| Icosahedron | 3 | 20 | 3/20 |
| 4-cube, 4D rectangular prism, 4D parallelepiped |
4 | 8 | 2/5 |
| 16-cell, aka cross polytope | 4 | 16 | 1/5 |
| 24-cell | 4 | 24 | 2/15 |
| 120-cell | 4 | 120 | 2/75 |
| 600-cell | 4 | 600 | 2/375 |
| d-cube, d-rectangular prism, d-parallelepiped |
d | 2d | 2 / (d+1) |
| d-dimensional cross polytope | d | 2d | 4 d / [(d+1) 2d] |
In the case of a square, there are only two possible ways that a line through two interior points can intersect the boundary: it can intersect two opposite sides, or two adjacent sides. Since we know that the probability of the first case is 2/3, the second case must occur the remaining 1/3 of the time, equally distributed with a probability of 1/12 between the four pairs of sides that meet at the four vertices.
In general, though, there will be more than two geometrically distinct outcomes.
In two dimensions, we will suppose the edges have lengths LA and LB, their directions are given by unit-length vectors A = (Ax, Ay) and B = (Bx, By) parallel to each edge, and the vector C = (Cx, Cy) points from the centre of the first edge to the centre of the second edge.
The 4-dimensional coordinates for a pair of points on a line segment joining these edges can then be given by:
P1,2(α, β, λ, μ) = ((1–λ) α A + λ (C + β B), (1–μ) α A + μ (C + β B))
where α ranges from –½LA to ½LA, β ranges from –½LB to ½LB, and λ and μ range from 0 to 1. The Jacobian matrix of partial derivatives of P1,2 with respect to these four parameters is:
| J | = |
|
The absolute value of the Jacobian determinant is:
|det(J)| = |(A × B) α + (B × C)| |(A × B) β + (A × C)| |μ – λ|
where we have defined a “two-dimensional cross product”:
u × v
= ux vy – uy vx
= |u| |v| sin θuv, given θuv is the counterclockwise angle from u to v.
We already know the integral of the last factor in |det(J)|:
∫01 ∫01 |μ – λ| dλ dμ = 1/3
In general, the other two integrals will have different results depending on whether or not the integrand crosses zero within the range of integration:
∫–½L½L |p α + q| dα
= |L q| [if p = 0 or –q/p ≤ –½L or –q/p ≥ ½L]
= |L2 p/4 + q2/p| [if –½L < –q/p < ½L]
Let’s apply this result to two edges of a regular n-gon of radius 1.
LA = LB = 2 sin(π / n)
θBC = θAC = π i / n
|C| = 2 cos(π / n) sin(π i / n)
B × C = A × C = |C| sin(π i / n) = 2 cos(π / n) sin(π i / n)2
We then have:
∫–½LA½LA |(A × B) α + (B × C)| dα
= | LA (B × C) |
= | 4 sin(π / n) cos(π / n) sin(π i / n)2 |
= 2 sin(2 π / n) sin(π i / n)2
The β integral is exactly the same. This gives us:
Vol4(n, i) = (4/3) sin(2 π / n)2 sin(π i / n)4
The area of the regular n-gon with unit radius is:
Area(n) = (n / 2) sin(2 π / n)
So we end up with the probability, for a specified pair of edges where the second edge is i steps around the n-gon from the first:
Prob1 edge pair(n, i)
= Vol4(n, i) / Area(n)2
= 16 / (3n2) sin(π i / n)4
= 4 / (3n2) (cos(2π i / n) – 1)2
There are n ways for two edges of an n-gon to be i steps apart, where i = 1, ..., floor(n/2), except when n is even and i = n/2, when there are n/2 ways. So when we count all edge pairs with a certain separation, rather than a specified edge pair, we have:
Probany edge pair(n, i)
= 4 / (3n) (cos(2π i / n) – 1)2 [i ≠ n/2]
= 8 / (3n) [i = n/2]
To generalise the two-dimensional case analysed in the previous section, we will suppose we have two (d–1)-dimensional faces in Rd, with the hyperplane containing the first face spanned by d–1 orthogonal unit vectors A1, ..., Ad–1, and the second face spanned by another set of orthogonal unit vectors B1, ..., Bd–1. We also have a vector C pointing from the centroid of the first face to the centroid of the second face. The (2d)-dimensional coordinates for a pair of points on a line segment joining the two faces are then given by:
P1,2(α1, ..., αd–1, β1, ..., βd–1, λ, μ) = ((1–λ) Σi=1d–1 αi Ai + λ (C + Σi=1d–1 βi Bi), (1–μ) Σi=1d–1 αi Ai + μ (C + Σi=1d–1 βi Bi))
We won’t try to show the whole Jacobian matrix. The Jacobian determinant ends up containing terms that are themselves the determinants of d × d matrices whose first d–1 rows are either the Ai or the Bi vectors, with some other vector as the last row, but these determinants are equal to ordinary dot products between the vector in question and unit normals to the first and second face respectively, so we will introduce those normal vectors, nA and nB. There is an ambiguity of sign in the choice of these normals, but it will make no difference to the final result.
With these extra definitions, the absolute value of the Jacobian determinant is:
|det(J)| = |μ–λ|d–1 | ((Σi=1d–1 αi Ai) – C) · nB | | ((Σi=1d–1 βi Bi) + C) · nA |
We previously evaluated the integral of the first factor as:
∫01 ∫01 |μ – λ|d–1 dλ dμ = 2 / [d (d+1)]
For the other factors, we integrate over a set of values for the α and β parameters that define the shape of the face. Because we have chosen an origin at the centroid, the first terms vanish, so long as the integrand does not change sign within the face. The results are then:
∫ Face 1 | ((Σi=1d–1 αi Ai) – C) · nB | = Area1 | C · nB |
∫ Face 2 | ((Σi=1d–1 βi Bi) + C) · nA | = Area2 | C · nA |
This gives a (2d)-dimensional volume of:
Vol2d = 2 Area1 Area2 | C · nA | | C · nB | / [d (d+1)]
In the context of a regular polytope with f congruent faces of area A, suppose the angle subtended at the centre of the polytope between the centroids of the two faces is θ, and the distance from the centre of the polytope to each centroid is h. The vector C joining the centroids is then the base of an isosceles triangle with two sides of length h and an angle of θ between them, with the other angles equal to (π – θ)/2. This gives us:
|C| = 2 h sin(θ/2)
| C · nA | = | C · nB | = |C| cos((π – θ)/2) = 2 h sin(θ/2)2
Vol2d = 8 A2 h2 sin(θ/2)4 / [d (d+1)]
= 2 A2 h2 (cos(θ) – 1)2 / [d (d+1)]
The volume of the whole polytope is f times the volume of a d-dimensional hyperpyramid with base A and height h:
Volpoly = f A h / d
This gives us the probability:
For any convex regular polytope in d dimensions with f faces, the probability that the line that passes through two randomly chosen points in the polytope will intersect a specific pair of faces whose centroids are separated by an angle of θ (as measured at the centre of the polytope) is:
Prob1 face pair(f, d, θ)
= Vol2d / Volpoly2
= 2 d (cos(θ) – 1)2 / [(d+1) f 2]
In an earlier section we found that the probabilities for all the pairs of opposite faces in a d-dimensional parallelepiped are equal, and are the same as those for a d-cube. This is also true for all the non-opposite pairs of faces. The simplest way to see this is to note that applying any invertible linear transformation T to a d-cube multiplies the volume by |det(T)|, while also multiplying the Jacobian determinant of the relevant function by |det(T)|2. Since we divide the Jacobian determinants by the squared volume of the parallelepiped to find the probabilities, the factors cancel out and the results are unchanged.
Similarly, because any nondegenerate simplex (a family of polytopes that includes triangles and tetrahedra) can be transformed by an invertible linear transformation into a regular simplex, the probabilities for all pairs of faces must be equal.
| Probability that the line that passes through two random points in a polytope intersects various pairs of faces | ||||||
|---|---|---|---|---|---|---|
| Polytope | Dimension d | Number of faces f | Type of face pair | Number of pairs of this type | Probability for one specific pair | Probability for any pair of this type |
| Any nondegenerate triangle | 2 | 3 | All | 3 | 1/3 | 1 |
| Square, rectangle, parallelogram | 2 | 4 | Opposite | 2 | 1/3 | 2/3 |
| Adjacent | 4 | 1/12 | 1/3 | |||
| Regular n-gon, even n | 2 | n | Opposite | n / 2 | 16 / (3n2) | 8 / (3n) |
| i steps apart, 1 ≤ i ≤ n/2–1 |
n | 4 / (3n2) (cos(2πi/n)–1)2 |
4 / (3n) (cos(2πi/n)–1)2 |
|||
| Regular n-gon, odd n | 2 | n | i steps apart, 1 ≤ i ≤ (n–1)/2 |
n | 4 / (3n2) (cos(2πi/n)–1)2 |
4 / (3n) (cos(2πi/n)–1)2 |
| Any nondegenerate tetrahedron | 3 | 4 | All | 6 | 1/6 | 1 |
| Cube, rectangular prism, parallelepiped | 3 | 6 | Opposite | 3 | 1/6 | 1/2 |
| Adjacent | 12 | 1/24 | 1/2 | |||
| Octahedron | 3 | 8 | Opposite | 4 | 3/32 | 3/8 |
| acos(–1/3) apart | 12 | 1/24 | 1/2 | |||
| acos(1/3) apart | 12 | 1/96 | 1/8 | |||
| Dodecahedron | 3 | 12 | Opposite | 6 | 1/24 | 1/4 |
| acos(–1/√5) apart | 30 | (3+√5)/240 | (3+√5)/8 | |||
| acos(1/√5) apart | 30 | (3–√5)/240 | (3–√5)/8 | |||
| Icosahedron | 3 | 20 | Opposite | 10 | 3/200 | 3/20 |
| acos(–(√5)/3) apart | 30 | (7+3√5)/1200 | (7+3√5)/40 | |||
| acos(–1/3) apart | 60 | 1/150 | 2/5 | |||
| acos(1/3) apart | 60 | 1/600 | 1/10 | |||
| acos((√5)/3) apart | 30 | (7–3√5)/1200 | (7–3√5)/40 | |||
| Any nondegenerate 4-simplex | 4 | 5 | All | 10 | 1/10 | 1 |
| 4-cube, 4D rectangular prism, 4D parallelepiped |
4 | 8 | Opposite | 4 | 1/10 | 2/5 |
| Adjacent | 24 | 1/40 | 3/5 | |||
| 16-cell, aka cross polytope | 4 | 16 | Opposite | 8 | 1/40 | 1/5 |
| 2π/3 apart | 32 | 9/640 | 9/20 | |||
| π/2 apart | 48 | 1/160 | 3/10 | |||
| π/3 apart | 32 | 1/640 | 1/20 | |||
| 24-cell | 4 | 24 | Opposite | 12 | 1/90 | 2/15 |
| 2π/3 apart | 96 | 1/160 | 3/5 | |||
| π/2 apart | 72 | 1/360 | 1/5 | |||
| π/3 apart | 96 | 1/1440 | 1/15 | |||
| 120-cell | 4 | 120 | Opposite | 60 | 1/2250 | 2/75 |
| 4π/5 apart | 720 | (3 + √5)/14400 | (3 + √5)/20 | |||
| 2π/3 apart | 1200 | 1/4000 | 3/10 | |||
| 3π/5 apart | 720 | (7 + 3 √5)/72000 | (7 + 3 √5)/100 | |||
| π/2 apart | 1800 | 1/9000 | 1/5 | |||
| 2π/5 apart | 720 | (3 – √5)/14400 | (3 – √5)/20 | |||
| π/3 apart | 1200 | 1/36000 | 1/30 | |||
| π/5 apart | 720 | (7 – 3 √5)/72000 | (7 – 3 √5)/100 | |||
| 600-cell | 4 | 600 | Opposite | 300 | 1/56250 | 2/375 |
| acos((–1 – 3 √5)/8) apart | 1200 | (7 + 3 √5)/800000 | 3 (7 + 3 √5)/2000 | |||
| acos((–5 – √5)/8) apart | 3600 | (87 + 13 √5)/7200000 | (87 + 13 √5)/2000 | |||
| 4π/5 apart | 7200 | (3 + √5)/360000 | (3 + √5)/50 | |||
| acos(–3/4) apart | 3600 | 49/3600000 | 49/1000 | |||
| acos((1 – 3 √5)/8) apart | 1200 | (47 + 21 √5)/7200000 | (47 + 21 √5)/6000 | |||
| acos((–3 – √5)/8) apart | 7200 | (63 + 11 √5)/7200000 | (63 + 11 √5)/1000 | |||
| acos(–1/4 √5) apart | 7200 | (21 + 8 √5)/3600000 | (21 + 8 √5)/500 | |||
| 2π/3 apart | 9600 | 1/100000 | 12/125 | |||
| acos((–1 – √5)/8) apart | 7200 | (43 + 9 √5)/7200000 | (43 + 9 √5)/1000 | |||
| acos((–5 + √5)/8) apart | 3600 | (87 – 13 √5)/7200000 | (87 – 13 √5)/2000 | |||
| 3π/5 apart | 7200 | (7 + 3 √5)/1800000 | (7 + 3 √5)/250 | |||
| acos(–1/4) apart | 8400 | 1/144000 | 7/120 | |||
| acos((1 – √5)/8) apart | 7200 | (27 + 7 √5)/7200000 | (27 + 7 √5)/1000 | |||
| acos((–3 + √5)/8) apart | 7200 | (63 – 11 √5)/7200000 | (63 – 11 √5)/1000 | |||
| π/2 apart | 16200 | 1/225000 | 9/125 | |||
| acos((3 – √5)/8) apart | 7200 | (3 + √5)/1440000 | (3 + √5)/200 | |||
| acos((–1 + √5)/8) apart | 7200 | (43 – 9 √5)/7200000 | (43 – 9 √5)/1000 | |||
| acos(1/4) apart | 8400 | 1/400000 | 21/1000 | |||
| 2π/5 apart | 7200 | (3 – √5)/360000 | (3 – √5)/50 | |||
| acos((5 – √5)/8) apart | 3600 | (7 + 3 √5)/7200000 | (7 + 3 √5)/2000 | |||
| acos((1 + √5)/8) apart | 7200 | (27 – 7 √5)/7200000 | (27 – 7 √5)/1000 | |||
| π/3 apart | 9600 | 1/900000 | 4/375 | |||
| acos(√5/4) apart | 7200 | (21 – 8 √5)/3600000 | (21 – 8 √5)/500 | |||
| acos((3 + √5)/8) apart | 7200 | (3 – √5)/1440000 | (3 – √5)/200 | |||
| acos((–1 + 3 √5)/8) apart | 1200 | (7 – 3 √5)/800000 | 3 (7 – 3 √5)/2000 | |||
| acos(3/4) apart | 3600 | 1/3600000 | 1/1000 | |||
| π/5 apart | 7200 | (7 – 3 √5)/1800000 | (7 – 3 √5)/250 | |||
| acos((5 + √5)/8) apart | 3600 | (7 – 3 √5)/7200000 | (7 – 3 √5)/2000 | |||
| acos((1 + 3 √5)/8) apart | 1200 | (47 – 21 √5)/7200000 | (47 – 21 √5)/6000 | |||
| Any nondegenerate d-simplex | d | d+1 | All | d(d+1)/2 | 2/(d(d+1)) | 1 |
| d-cube, d-rectangular prism, d-parallelepiped |
d | 2d | Opposite | d | 2 / (d(d+1)) | 2 / (d+1) |
| Adjacent | 2d (d–1) | 1 / (2d(d+1)) | (d–1) / (d+1) | |||
| d-dimensional cross polytope | d | 2d | Opposite | 2d–1 | 8 d / [(d+1) 22d] | 4 d / [(d+1) 2d] |
| acos(2a/d – 1) apart a = 1, ..., d–1 |
2d–1 Binomial(d, a) | 8 (a – d)2 / [d(d+1) 22d] | 4 (a – d)2 Binomial(d, a) / [d(d+1) 2d] | |||
Suppose we pick two points uniformly at random in the interior of a disk, then draw a line through both points and see where it intersects the boundary of the disk.
If we parameterise the pair of interior points according to the angular positions of the line’s endpoints and the position of each interior point on the line, we have:
P1,2(α, β, λ, μ) = ((1–λ) (cos α, sin α) + λ (cos β, sin β), (1–μ) (cos α, sin α) + μ (cos β, sin β))
Here α, β range from 0 to 2π and λ, μ range from 0 to 1. The absolute value of the Jacobian determinant is:
|det(J)|
= 4 |μ–λ| sin((α–β)/2)4
= |μ–λ| (cos(α–β) – 1)2
We can integrate over λ and μ and divide by the squared area of the unit disk to obtain the probability density function:
PDFendpoints(α, β) = (cos(α–β) – 1)2 / (3π2)
We need to treat this probability density function carefully. If we integrate over the full range for both α and β it will give a result of 2, not 1, because each pair of points in the disk will appear twice, with the two endpoints of the line ascribed to the α and β coordinates in either of two ways. And if we ask about the probability of the pair of points yielding a line that has both endpoints on any particular arc, we need to integrate over that arc for both α and β, but then halve the result. But for two completely disjoint arcs, we simply integrate over the separate angular ranges for α and β.
As an example, suppose we divide up the boundary of the disk into n equal-sized arcs. The probability of the line intersecting two different specific arcs, where one of them is the jth neighbour of the other, can be found by integrating this PDF across suitable angles for α and β. This comes to:
P1 arc pair(n, j) = 2/n2 + (cos(2δ j) sin(δ)2 – 16 cos(δ j) sin(δ/2)2) / (6π2)
where δ = 2π/n
But the probability for the line having both endpoints on any specific single arc is found by setting j = 0 in this formula then halving the result:
P1 arc(n) = 1/n2 + (sin(δ)2 – 16 sin(δ/2)2) / (12π2)
= 1/n2 – sin(δ/2)2 (3 + sin(δ/2)2) / (3π2)
For a disk with no special features marked, we can still ask about the probability distribution for the angle between the endpoints of the line. Taking this to be the smaller of the two angles, i.e to lie between 0 and π, we can obtain this from our previous PDF for the two endpoint locations as:
PDFangle(γ) = 2/(3π) (cos(γ) – 1)2
with a corresponding cumulative distribution function:
CDFangle(γ)
= ∫ PDFangle(γ) dγ
= γ/π + (sin(2γ) – 8 sin(γ)) / (6π)
As an example, we have:
Prob(γ > 2π/3) = 1 – CDFangle(2π/3)
= 1/3 + (3√3) / (4π)
≈ 0.74683
(This is one more way to answer the question: “What is the probability that a random chord on a circle spans a greater angle than the chords of an inscribed equilateral triangle?” — which famously gives different answers depending on exactly how you construct the random chord, an observation known as Bertrand’s paradox.)
We can perform a similar calculation for a three-dimensional ball. We parameterise the endpoints of the line segment on the boundary of the unit-radius ball with two standard polar coordinates θ and φ each, and the two points in the interior with our usual λ and μ coordinates. We then compute a 6 × 6 Jacobian matrix for the pair of interior points in Cartesian coordinates with respect to θ1, φ1, θ2, φ2, λ and μ, but then for the sake of simplicity set θ1 = θ2 = π/2 (i.e. both endpoints are on the equator) and φ1 = 0, φ2 = γ, the angular separation between the endpoints. The Jacobian determinant is:
|det(J)| = (μ–λ)2 (cos(γ) – 1)2
We find the probability density function for γ by integrating over λ and μ from 0 to 1, multiplying by 4π (for the first endpoint moving over the whole sphere), 2π sin(γ) (for the second endpoint rotating around the first while staying at an angle of γ), 1/2 (to avoid double counting configurations where the endpoints are swapped), and dividing by (4π/3)2, for the total volumes the interior points are selected from.
The result is:
PDFangle, sphere(γ) = (3/8) (cos(γ) – 1)2 sin(γ)
This is easily integrated to obtain the CDF:
CDFangle, sphere(γ) = (1/8) (1 – cos(γ))3
In this case, the probability that the chord spans an angle greater than 120° is:
Prob(γ > 2π/3) = 1 – CDFangle, sphere(2π/3)
= 1 – 27/64
= 37/64
= 0.578125
|
|
|