Reptends and Reciprocals

by Greg Egan

• Symmetries and the 24-cell | Average Shadows | Ball Bearings in a Hypersphere | Black Hole Passing | Born Rigid Motion | Catacaustics | Resonant Modes of a Conical Cavity | The Doppler Shift Triangle Law | Conic Section Orbits | Double-Crossing Orbits | Dihedral Angles | The Ellipse and the Atom | Find The Fake Coin | The Finite Fall | General Relativity in 2+1 dimensions | Howell’s Moving Orbits | Klein's Quartic Curve | Paparazzo vs Bodyguards | Light Mill applet | Littlewood applet | LRL made easy | The Mermin-Peres Magic Square Game | There Are No Corkscrew Orbits | Peeling the Octonions | Ordered Sums | Optimised Origami | Pick Two Points | Weak-field GR near a planar mass | Polar Orbits Around Binary Stars | Planes, Spheres and Pseudospheres | Reptends and Reciprocals | The Rindler Horizon | Rotating Elastic Rings, Disks and Hoops | Constant Weight Rollercoasters | Steffen’s Polyhedron | Superpermutations | Symmetric Waves | Symplectic applet | The Tell-Tale Board | Exact values of regular 10j symbols
• Science Notes
• Back to home page | Site Map | Side-bar Site Map

• Reciprocals with Non-Redundant Pandigital Reptends
• From Repeating Digits to Rational Numbers
  • Excluding the Odd Bases
  • Even Bases
    • Bases that are Powers of Two
    • Other Even Bases
• From Reciprocals to Repeating Digits
  • The Long Division Algorithm
  • The Ring Z_n and the Group Z_n^×
  • Base and Divisor are Coprime
  • Base and Divisor have Common Factors

Reciprocals with Non-Redundant Pandigital Reptends

Is there an integer d whose reciprocal, 1/d, has a decimal representation with a recurring block of digits exactly 10 digits long, containing all ten decimal digits?

The answer is yes! 72,728 has this property. In fact, we can find integers with analogous properties in several different bases besides base 10. A number is described as pandigital in base b if its representation contains all the digits 0, ..., b – 1, and non-redundant if each digit appears only once, so we will call these blocks of b repeating digits, enclosed in parentheses in the table below, non-redundant pandigital reptends.

Here we are describing the integers themselves with the usual base 10 notation, and only switching to base b when we give the representations of the fractions. We follow the convention of using the letters A, B, C, ... for digits 10, 11, 12, ... in bases greater than 10.

These numbers were found with a computer search, which came up empty for all the other bases that were tried. But are these really the only bases in which an integer can have this property?

Question: In what bases can the reciprocal of an integer have a non-redundant pandigital reptend?

Partial answer: We will prove with some simple number theory that there are no solutions for odd bases. Computer calculations have ruled out any solutions for bases that are powers of two from 8 to 8192, as well as providing the particular solutions given in the table above.

But in general, this is still an open question.

[If we didn’t care about the non-redundancy of the digits, this would be a trivial question: for every base there are an infinite number of integers whose reciprocals have pandigital reptends, when some digits are allowed to appear more than once. The Online Encyclopedia of Integer Sequences (OEIS) has a list of the smallest such integers for each base, A382498.]

From Repeating Digits to Rational Numbers

One step towards answering this question is to look at the rational number we get if we are provided with the representation of a number in base b in the following form:

0 . k-digit prefix x j-digit reptend r j-digit reptend r ...

Here k, the length of the non-repeating portion of the number, can be zero, but we will assume that j, the length of the reptend, is at least 1. By x and r we mean the integers whose digits slot into this pattern, with 0 ≤ x < b^k and 0 ≤ r < b^j.

The rational number R that this represents can be found by summing a geometric series with an infinite number of terms:

R = [x + r Σ_{i = 1}^∞ (1 / b^j)ⁱ] / b^k
= [x + (r / b^j) 1 / (1 – 1 / b^j)] / b^k
= [x + r / (b^j – 1)] / b^k

We can check this formula with a few examples:

R = 0.(142857) ...
b = 10
r = 142,857
j = 6
x = k = 0

R = 142,857 / (10⁶ – 1) = 142,857 / 999,999 = 1/7

R = 0.03(571428) ...
b = 10
r = 571,428
j = 6
x = 3
k = 2

R = (3 + 571,428 / (10⁶ – 1)) / 10²
= (3 + 571,428 / 999,999) / 100
= (3 + 4/7) / 100
= 25/700
= 1/28

R = 0.0(0132)₄ ...
b = 4
r = 132₄ = 2 + 3×4 + 1×4² = 30
j = 4
x = 0
k = 1

R = (30 / (4⁴ – 1)) / 4
= (30 / 255) / 4
= 1/34

Since we will mostly be concerned with rational numbers that are reciprocals of integers, we will find it useful to rewrite this formula as:

When R = 1/d:

d [r + x (b^j – 1)] = (b^j – 1) b^k

Excluding the Odd Bases

Let’s return to our original question about which bases allow reciprocals of integers to have non-redundant pandigital reptends. We will be performing several calculations in modular arithmetic, with modulus b – 1. We start with a couple of obvious statements:

b ≡ 1 (mod b – 1)
bⁱ ≡ 1 (mod b – 1) for any integer i

This in turn means that any number with digits D_i is equivalent, mod b – 1, to the sum of its digits:

Σ_i=0ⁿ D_i bⁱ ≡ Σ_i=0ⁿ D_i (mod b – 1)

This is the basis for the well-known divisibility tests for 3 and 9: a number in base 10 will be equivalent to the sum of its digits, modulo 9.

For a non-redundant pandigital integer P_b in base b, since its digits are 0, ..., b – 1 (in any order, it doesn’t matter), we have:

P_b ≡ Σ_i=0^{b – 1} i ≡ ½ b (b – 1) (mod b – 1)

Now, suppose the base b is odd. Then b – 1 is even, and we have:

P_b ≡ ½(b – 1) (mod b – 1, for b odd)

For example, if b = 7, then for any non-redundant pandigital number in base 7, with 0+1+2+3+4+5+6 = 21:

P₇ ≡ ½(b – 1) ≡ 3 (mod 6)

If we take our formula linking an integer d with the features of its reciprocal’s representation in base b, and assume that the reptend r is a non-redundant pandigital number in an odd base, we get:

For odd base b, and a non-redundant pandigital reptend r for the reciprocal of d:

r ≡ ½(b – 1) (mod b – 1)

d [r + x (b^b – 1)] = (b^b – 1) b^k
d r = (b^b – 1) (b^k – d x)
d r = (b – 1) (1 + b + b² + ... + b^{b – 1}) (b^k – d x)

The reptend r is not divisible by b – 1, so d must be. Suppose d = g (b – 1), and divide both sides of the equation by b – 1.

g r = (1 + b + b² + ... + b^{b – 1}) (b^k – g (b – 1) x)

Now taking everything mod b – 1:

g (½(b – 1)) ≡ (1 + 1 + ... [b terms]) (1 – 0) ≡ 1 (mod b – 1)

If g is even, then g (½(b – 1)) ≡ 0 (mod b – 1), so g must be odd. But in that case, g (½(b – 1)) ≡ ½(b – 1), leaving us with:

½(b – 1) = 1
b = 3

So we have ruled out all odd bases except for b = 3. But our computer search found no reciprocals with non-redundant pandigital reptends in base 3. Can we prove that this is also impossible?

The non-redundant pandigital integers in base 3 are:

{012₃, 021₃, 102₃, 120₃, 201₃, 210₃}
= {5, 7, 11, 15, 19, 21}

Note that all of these values are odd.

Our formula linking the integer d with the representation of its reciprocal becomes:

d [r + x (b^b – 1)] = (b^b – 1) b^k
d [r + 26 x] = 26 × 3^k = 2 × 13 × 3^k

Since r must be odd, the only possible prime factors of r + 26 x are 3 and 13. If we first assume no factor of 13, we have:

r + 26 x ≡ r ≡ 3^a (mod 13)

But since 3³ = 27 ≡ 1 (mod 13), the only powers of 3 are {1, 3, 9} (mod 13), whereas our list of possible values of r is:

{5, 7, 11, 15, 19, 21} ≡ {5, 7, 11, 2, 6, 8} (mod 13)

On the other hand, if we assume r + 26 x does have a factor of 13, then so will r. But none of the possible values of r satisfies this condition either.

So we have proved:

Theorem 1: In any odd base, no integer has a reciprocal with a non-redundant pandigital reptend.

Even Bases

Now, suppose the base b is even. We then have, for any non-redundant pandigital integer:

P_b ≡ ½ b (b – 1) ≡ 0 (mod b – 1, b even)

For example, if b = 10, then for any non-redundant pandigital number in base 10, with 0+1+2+3+4+5+6+7+8+9 = 45:

P₁₀ ≡ 0 (mod 9)

For even b, we can factor b^b – 1 as:

b^b – 1 = (b^½b – 1) (b^½b + 1)

The two factors here are both odd and differ by two, so they must be coprime: they cannot have any factors in common. We can then go further with the first factor:

b^½b – 1 = (b – 1) (1 + b + b² + ... + b^{½b – 1})

Again, these two factors must be coprime, because modulo any factor f of b – 1, where f > 1, we have:

b – 1 ≡ 0 (mod f)
b ≡ 1 (mod f)
bⁱ ≡ 1 (mod f) for any integer i
1 + b + b² + ... + b^{½b – 1} ≡ ½b (mod f)

Combining these results:

b^b – 1 = (b – 1) (1 + b + b² + ... + b^{½b – 1}) (b^½b + 1)

where all three factors on the right-hand side are mutually coprime.

If our reptend r is a non-redundant pandigital integer, we have:

For even base b, and a non-redundant pandigital reptend r for the reciprocal of d:

r = (b – 1) s, for some integer s

(b^b – 1) = (b – 1) (1 + b + b² + ... + b^{½b – 1}) (b^½b + 1)

d [r + x (b^b – 1)] = (b^b – 1) b^k
d [(b – 1) s + x (b – 1) (b^b – 1)/(b – 1)] = (b – 1) (1 + b + b² + ... + b^{½b – 1}) (b^½b + 1) b^k
d [s + x (b^b – 1)/(b – 1)] = (1 + b + b² + ... + b^{½b – 1}) (b^½b + 1) b^k

To search for solutions for a fixed choice of b and k, we can factor the right-hand side of the last equation above, (1 + b + b² + ... + b^{½b – 1}) (b^½b + 1) b^k, into individual prime factors, which must then be allocated between the two algebraic factors on the left-hand side, d and [s + x (b^b – 1)/(b – 1)]. This lets us enumerate all the possible values for:

r + x (b^b – 1) = (b – 1) [s + x (b^b – 1)/(b – 1)]

and we can extract r alone by taking that quantity and computing the remainder mod b^b – 1.

Note that b is coprime with b^b – 1, so all three algebraic factors on the right-hand side are mutually coprime.

We can immediately rule out any allocation where the second algebraic factor, [s + x (b^b – 1)/(b – 1)], ends up as a multiple of b^½b + 1, as this would leave us with a reptend whose first ½b digits were identical to its last ½b digits. For example, for b = 8, we have b^½b + 1 = 10001₈, and clearly any multiple of this (mod b^b – 1) would have its first four digits identical to its last four digits.

So at least one of the prime factors of b^½b + 1 must be allocated to d, or r will contain repeated digits, ruling it out as a valid solution.

We can also rule out any allocation where d is divisible by b, not because the result would be invalid, but because it would be redundant. Multiplying a solution for d by any power of b will give another solution, as will dividing out any powers of b, but it is more efficient just to search for the single member of that family of solutions where d is not divisible by b at all.

Bases that are Powers of Two

For the special case where b is a power of 2, this search becomes a great deal simpler. Suppose b = 2^t, and so b^b = 2^{2t t}. We then have:

2^{2t t} ≡ 1 (mod b^b – 1)

and so doubling any number 2^t t times (mod b^b – 1) will always cycle back to the original value.

In fact, multiplying by 2 (mod b^b – 1) is exactly the same as rotating the (2^t t)-bit binary representation of the number left by one bit, with the most significant bit rotated into the least significant bit. And because the property of being non-redundantly pandigital or not is unchanged if we rotate by a whole digit, i.e. by t bits, we only need to take each proper divisor of (b^b – 1)/(b – 1) that is not a multiple of b^½b + 1, multiply it by b – 1, then check the rotations by between 0 and t–1 bits to see if any of them yield solutions.

Because b is a power of 2, we can factor (b^b – 1)/(b – 1) much further algebraically than in the general case.

(b^b – 1)/(b – 1) = (b + 1) (b² + 1) (b⁴ + 1) ... (b^¼b + 1) (b^½b + 1)

All the algebraic factors on the right-hand side turn out to be mutually coprime. To see this, choose any two factors with powers of b of m and n, with m < n, and note that n/m will be an even integer. Suppose f > 1 divides b^m + 1, which is odd, so f ≠ 2. We then have:

b^m + 1 ≡ 0 (mod f)
b^m ≡ –1 (mod f)
bⁿ ≡ (–1)^n/m ≡ 1 (mod f)
bⁿ +1 ≡ 2 ≢ 0 (mod f)

In most cases we can go even further. Note that for any odd power n > 1 (and where y is just a variable):

yⁿ + 1 = (y + 1) A_n–1(y)
where we define A_a(y) = 1 – y + y² – ... + (–y)^a

The first factor on the right-hand side, y + 1, shares the obvious zero of y = –1 with the left-hand side, while the second factor, A_n–1(y), has as zeroes the remaining nth roots of –1:

y_j = –exp(2 π j i / n),    j = 1, ..., n–1

If n is prime the right-hand side can’t be factored any further. But suppose n is divisible by p^s for some prime p. In this case, we can always extract s factors of the form:

A_p–1(y^pw),   for w = 0, ..., s–1

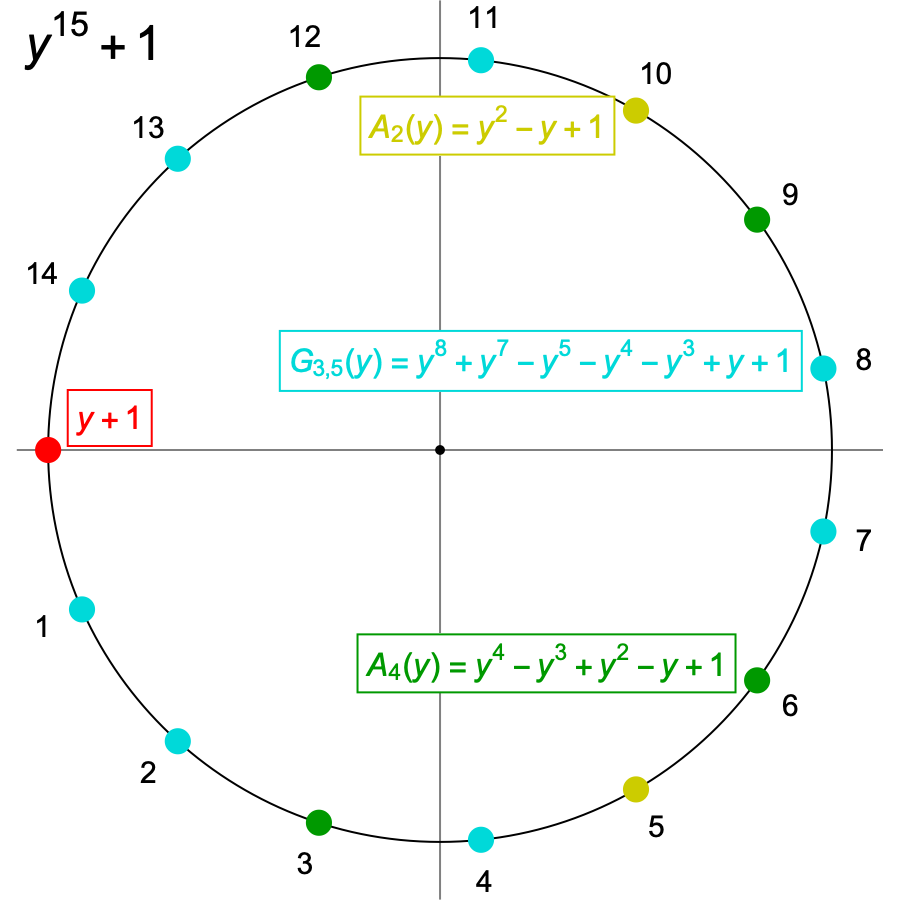
For example, for n equal to the following powers of 3, we have factors of A₂(y), A₂(y³) and A₂(y⁹).

y³ + 1 = (y + 1) (1 – y + y²)
y⁹ + 1 = (y + 1) (1 – y + y²) (1 – y³ + y⁶)
y²⁷ + 1 = (y + 1) (1 – y + y²) (1 – y³ + y⁶) (1 – y⁹ + y¹⁸)

For n = 27, the nth roots of –1 are shared between the factors as shown in the image below. The numbers here correspond to the indices for the roots y_j we defined earlier.

We see that:

• the two zeroes of A₂(y) are the two cube roots of –1 other than –1 itself,
• the six zeroes of A₂(y³) are all the cube roots of those two cube roots [making them ninth roots of –1, but none of them are also cube roots of –1],
• the eighteen zeroes of A₂(y⁹) are all the ninth roots of those two cube roots [making them 27th roots of –1, but none of them are also 9th roots of –1].

So there are no overlaps between these subsets of the 27th roots of –1, and along with –1 itself they account for all 27.

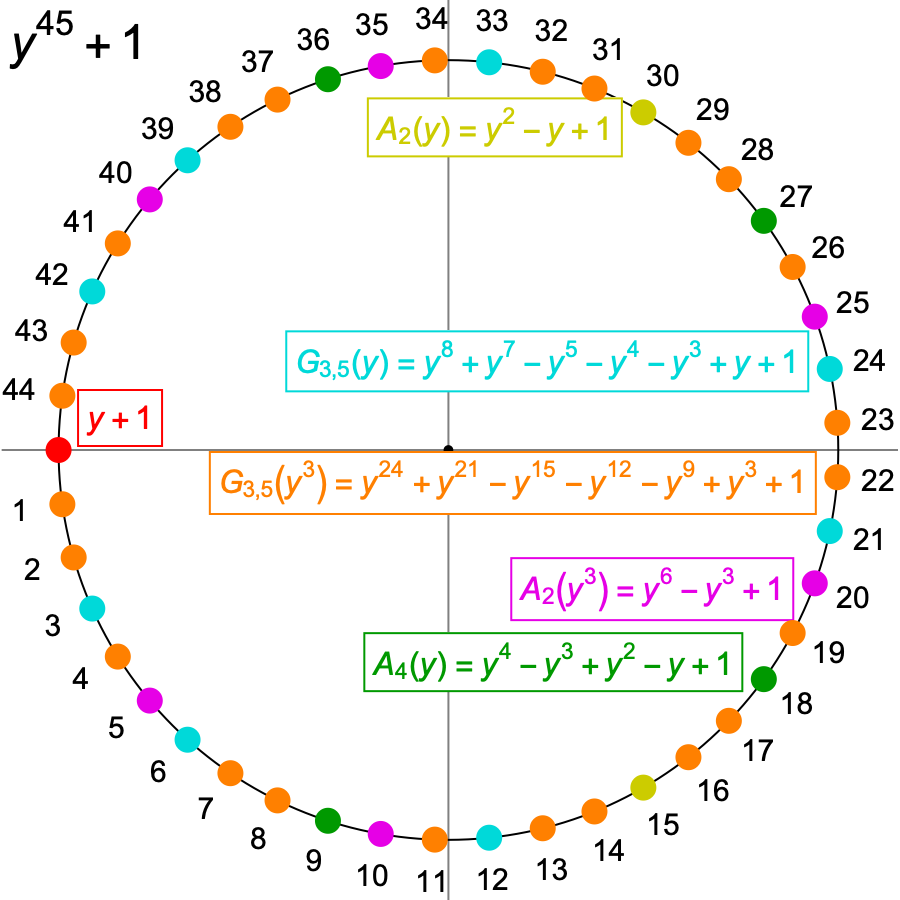
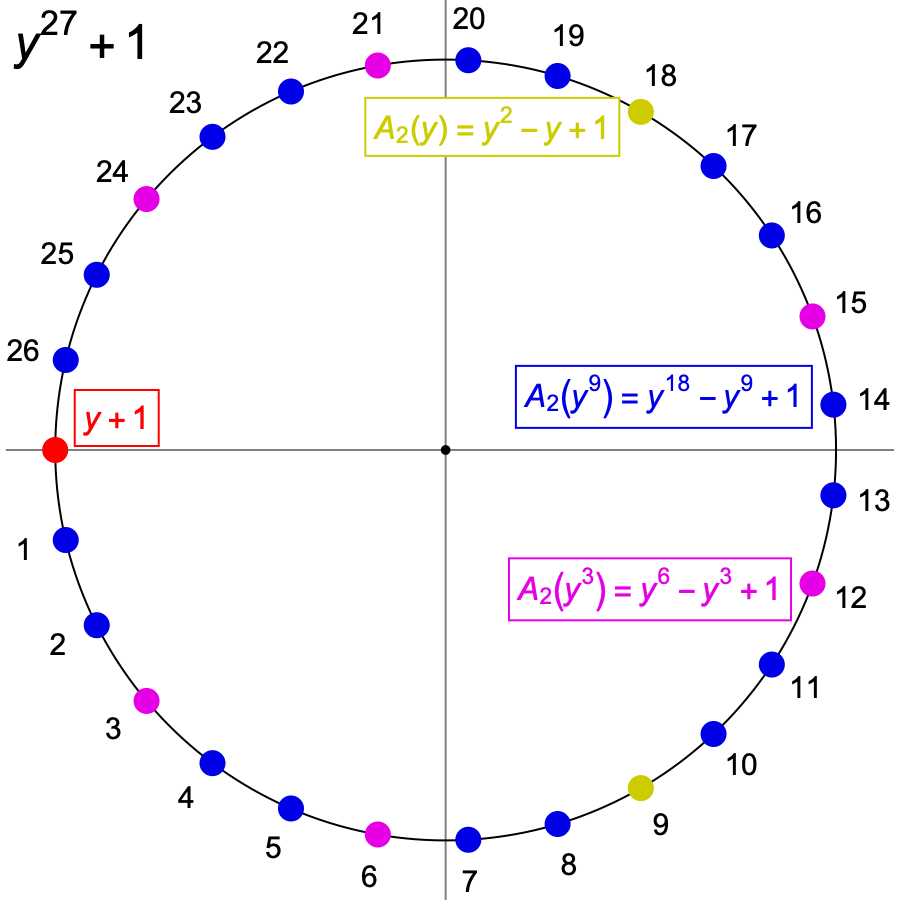
What if n has several distinct prime factors? Then yⁿ + 1 must still have the factors A_p–1(y^pw), w = 0, ..., s–1 for each prime factor p where p^s divides n, but they will not account for all the roots, so there must be another factor or factors that include them. For example, here are the roots for n = 15 and n = 45, shared between the factors:

What can we say about the factors left over when we have divided out all the A_p–1(y^pw)?

We will define the polynomial:

G_{a, b, c, ...}(y) = gcd(A_a–1(y^{bc ...}), A_b–1(y^{ac ...}), A_c–1(y^{ab ...}), ...)

Here, the gcd is the greatest common divisor of the polynomials listed, i.e. the polynomial of highest degree that divides all of them, and which has as its zeroes all the zeroes that the listed polynomials have in common. We will remove a potential ambiguity by requiring the coefficient of the highest power of the variable in the gcd to be +1.

So, G_{3, 5}(y) has as its zeroes all the zeroes that A₂(y⁵) and A₄(y³) have in common, which are precisely the 15th roots of –1 that are neither fifth roots nor cube roots of –1.

Similarly, G_{3, 5}(y³) has as its zeroes the 45th roots of –1 that are neither 15th roots nor 9th roots of –1.

In general, we can factor yⁿ + 1 by associating a factor with each divisor of n, as follows:

• With the divisor 1, we associate the factor y+1.
• With a divisor d that is the product of primes p₁^k₁ p₂^k₂ ... we associate the factor G_{p1, p2, ...}(y^{p₁k₁–1 p₂k₂–1 ...}), where in the case that there is just one prime p in the divisor, the gcd is superfluous and G_p is just A_p–1. The zeroes of this factor are all dth roots of –1 that are not also (d/p_i)th roots for any of the prime factors p_i of d, which is equivalent to saying that they are not qth roots of –1 for any proper divisor q of d.

Now, while the powers of b that appear in the terms b^z + 1 in our factorisation of (b^b – 1)/(b – 1):

(b^b – 1)/(b – 1) = (b + 1) (b² + 1) (b⁴ + 1) ... (b^¼b + 1) (b^½b + 1)

are all powers of 2, so we have z = 2^v for some v, so long as t is not also a power of 2 we will have:

t = n 2^u for some odd n > 1
b^z = b^2v = (2^{n 2u})^2v = (2^2u+v)ⁿ

So we can set y = 2^2u+v and apply our algebraic factorisations of yⁿ + 1 for odd n. Of course this will generally not fully factor the integers in question, and unlike the previous stage, there is no guarantee that the integers we get from these algebraic factors will be mutually coprime.

Before performing any rotations of divisors, we can reject some candidates completely:

• The longest possible run of consecutive zero bits in a non-redundant pandigital integer for base b = 2^t will be 3t–2, arising when the digit 0 is preceded by the digit 2^t–1 and followed by the digit 1. So we can rule out any candidate that is less than 2^{(2t – 3) t + 1}.
• For any non-redundant pandigital integer, the total number of bits that are equal to 1 in each of the t bit positions across all b digits is ½b. Since all of these totals are the same, they remain the same under a bitwise rotation, so we can rule out any candidate that fails to meet this condition.

For example:

t = 2
b = 2^t = 4
2^t t = 8
b^b – 1 = 4⁴ – 1 = 255
b^½b + 1 = 17
2^{(2t – 3) t + 1} = 2³ = 8.

Proper divisors of 255 / 3 = 85 are: 1, 5, 17.
Ruling out multiples of b^½b + 1 = 17 leaves: 1, 5.
Multiplying by 3 gives: 3, 15.
Ruling out candidates less than 8 leaves: 15.
In base 4, this is: 0033₄.
0033₄ has 2 out of 4 of the bits equal to 1 in each bit position.
Rotated 1 bit to the left, 0033₄ becomes: 0132₄.
0132₄ is non-redundantly pandigital, so we have a solution:
d = (b^b – 1) b^k / 0132₄ = 255 × 4 / 30 = 34

t = 3
b = 2^t = 8
2^t t = 24
b^b – 1 = 8⁸ – 1 = 16,777,215
b^½b + 1 = 4097
2^{(2t – 3) t + 1} = 2¹⁶ = 65,536.

There are 47 proper divisors of 16,777,215 / 7 = 2,396,745:

1, 3, 5, 9, 13, ... 798,915.

Ruling out multiples of b^½b + 1 = 4097 leaves 36 candidates:

1, 3, 5, 9, 13, ... 140,985.

Multiplying by 7 gives: 7, 21, 35, ... 986,895.
There are 7 candidates greater than or equal to 65,536:

65,793, 69,615, 75,915, 109,655, 197,379, 328,965, 986,895.

In base 8, these are:

00200401₈, 00207757₈, 00224213₈, 00326127₈, 00601403₈, 01202405₈, 03607417₈.

The count of 1s in each of the bit positions are:

(1,1,1), (4,4,4), (1,4,2), (2,5,3), (2,2,2), (2,2,2), (4,4,4)

Ruling out candidates with the wrong number of bits equal to 1 leaves:

00207757₈, 03607417₈.

But rotating these two numbers by 0, 1 or 2 bits produces no solutions.

For large values of b, factoring (b^b – 1)/(b – 1) in order to list all its divisors is not a very efficient approach to identifying the candidates we want. But we can also generate candidates, c, by finding the numbers q, the partners of c in the product c q = b^b – 1, that satisfy the following conditions:

• q ≤ 2^{3t – 1}
• q is a product of a divisor greater than 1 of b^½b + 1, and any divisor of (b^½b – 1) / (b – 1).

For example:

t = 3
b = 2^t = 8
b^b – 1 = 8⁸ – 1 = 16,777,215
b^½b – 1 = 8⁴ – 1 = 4095
b^½b + 1 = 8⁴ + 1 = 4097
2^{3t – 1} = 2⁸ = 256.

The factors of b^½b + 1 = 4097 are: 17, 241.
The factors of (b^½b – 1) / (b – 1) = 4095 / 7 = 585 are: 3², 5, 13.
Multiples of 17 or 241 that do not exceed 256, using divisors of 585, are:

17, 3 × 17 = 51, 5 × 17 = 85, 3² × 17 = 153, 13 × 17 = 221, 241, 3 × 5 × 17 = 255

Dividing b^b – 1 by these numbers gives the seven candidates we found previously.

In this second way of analysing the t = 3 case, the two values for q that correspond to values of c with the correct bit counts are 17 and 241, which are divisors of b^½b + 1 but contain no factors from (b^½b – 1) / (b – 1), which guarantees that the c values are multiples of b^½b – 1. This is not a coincidence; any multiple of b^½b – 1 = 7777₈ = 10000₈ – 1₈ by a number less than b^½b + 1 = 10001₈, will have its first four digits (if we treat it as an eight-digit octal number, padded on the left with zeroes if necessary) and the corresponding digits in the last four adding up to 7, which will ensure the correct bit counts. For example:

7777₈ × 1234₈
= (10000₈ – 1₈) × 1234₈
= 12340000₈ – 1234₈
= 12336544₈

But while this restriction on q is sufficient to guarantee correct bit counts, it is not necessary. For example, for t = 13, q = 1,084,030,993 corresponds to a value of c with correct bit counts, but this q is a product of 63,766,529, a divisor of b^½b + 1, and 17, a divisor of b^½b – 1. Another case, again for t = 13, is q = 2,211,512,405, which is a product of 26,017,793 as the divisor of b^½b + 1, and 5 × 17 as the divisor of b^½b – 1.

If it is obvious why multiples of b^½b – 1 give us the correct bit count, what’s going on here? In hexadecimal, the values of b^½b – 1 divided by 17 and 5 × 17 are:

t = 13
b = 2¹³ = 8192
(b^½b – 1) / 17 = 0F₁₆ ... repeated 6656 times
(b^½b – 1) / (5 × 17) = 03₁₆ ... repeated 6656 times

6656 = 512 × 13, so 2 × 6656 hex digits = 4096 base-2¹³ digits

These two numbers actually have bit counts for all 13 bits of the base-2¹³ digits of 2048 and 1024 respectively, rather than the required 4096. While we have some specific (very large) multiples of each with the correct bit counts, those numbers display no simple, obvious symmetry that accounts for the property.

Another approach (much cruder, but conceptually simpler) is to note that, if any solution that exists will be found by taking a factor of at most 2^t–1 from b^k for the term [r + x (b^b – 1)], we only need to consider the cases where k is either 0 or 1, so the prefix part of the representation of the reciprocal is at most one digit. If the reptend is non-redundantly pandigital, this in turn means that:

1/d ≥ 0.0(012...[b–1])_b ...

So, rounding up for the sake of simplicity:

d < b³

Checking the base-b representations of the reciprocals of all integers that meet this bound offers another way to find, or rule out, solutions for the special cases where b is a power of 2. For the case b = 4, the solution corresponds to d = 34, which satisfies the bound.

If we return to the equation:

d [s + x (b^b – 1)/(b – 1)] = (1 + b + b² + ... + b^{½b – 1}) (b^½b + 1) b^k

and take mod b – 1 of both sides, we get:

d [s + x] ≡ 1 (mod b – 1)

This is only possible if d and s + x are both coprime with b – 1; that is, neither of them are divisible by any number greater than 1 that also divides b – 1, because modulo any such factor the left-hand side here would be 0 and the right-hand side 1. So in our search for possible values for d, we can rule out any numbers that share factors greater than 1 with b – 1.

Either approach can be used to exhaustively check all the candidates for several bases, up to the point where the calculations become impractical. As it turns out, this shows that there are no solutions for bases that are powers of two from 8 up to at least 8192.

Theorem 2: In all bases that are powers of two from 8 to 8192, no integer has a reciprocal with a non-redundant pandigital reptend.
Proof: Direct examination by computer of all candidate reptends.

Other Even Bases

For an arbitrary even base, there is no obvious ceiling on the total number of reptends that might need to be examined [other than b^b – 1, which is too large to be practical for most bases], so without further theoretical justification, we can’t claim to have ruled out solutions for any even base that is not a power of 2. Similarly, in most of the cases where we have found solutions, we can’t be sure that the integer we have found for d is the smallest one possible. The exceptions are when d is small enough that we can check all integers up to d individually.

From Reciprocals to Repeating Digits

The Long Division Algorithm

Let’s take a look at the reverse of the process we considered in the previous section. Given a reciprocal of an integer, 1/d, what is the prefix x of length k and reptend r of length j that are produced in base b?

Of course the algorithm that produces these things is just long division, but because most people learn how to do this at a very young age and never revisit it, a lot of the richness and subtlety of the underlying mathematics passes us by.

Let’s examine what happens when we use long division to find the decimal representations of 1/13 and 1/28.

0.076923... 13 | 1.000000000 –0 (0 × 13) 100 –91 (7 × 13) 90 –78 (6 × 13) 120 –117 (9 × 13) 30 –26 (2 × 13) 40 –39 (3 × 13) 10

0.03571428... 28 | 1.000000000 –0 (0 × 28) 100 –84 (3 × 28) 160 –140 (5 × 28) 200 –196 (7 × 28) 40 –28 (1 × 28) 120 –112 (4 × 28) 80 –56 (2 × 28) 240 –224 (8 × 28) 160

Starting with the number 1, we multiply the current remainder by 10, find the largest multiple of the divisor, d, that it contains, record the multiplier as the digit in the quotient, then continue with the new remainder we obtain by subtracting that multiple of d.

For d=28, because we return to a remainder of 16, rather than 1, the digits do not repeat from the start; the digits 03 form a non-repeating prefix, while 571428 is the reptend.

The remainders here are just the powers of the base, 10, modulo the divisor.

10⁰ ≡ 1
10¹ ≡ 10 = 0 × 13 + 10
10² ≡ 100 = 7 × 13 + 9
10³ ≡ 90 = 6 × 13 + 12
10⁴ ≡ 120 = 9 × 13 + 3
10⁵ ≡ 30 = 2 × 13 + 4
10⁶ ≡ 40 = 3 × 13 + 1

10⁰ ≡ 1
10¹ ≡ 10 = 0 × 28 + 10
10² ≡ 100 = 3 × 28 + 16
10³ ≡ 160 = 5 × 28 + 20
10⁴ ≡ 200 = 7 × 28 + 4
10⁵ ≡ 40 = 1 × 28 + 12
10⁶ ≡ 120 = 4 × 28 + 8
10⁷ ≡ 80 = 2 × 28 + 24
10⁸ ≡ 240 = 8 × 28 + 16

The Ring Z_n and the Group Z_n^×

To understand the kinds of sequences that the powers of a base, b, can produce modulo the divisor, d, we need to delve a little further into the algebraic structure that underlies modular arithmetic.

When we are performing modular arithmetic on the n integers 0, 1, ..., n–1, we refer to this set as Z_n. If we are only interested in addition, Z_n becomes what is known as a commutative group: a set with a single operation, +, that obeys all the usual rules for adding numbers, including the existence of an additive identity, 0, which leaves things unchanged when you add it, and additive inverses for every number x in the set, which you can add to x to get 0. In this case, we have:

x + (n–x) ≡ 0 (mod n)

If we also wish to perform multiplication, things become a bit more complicated. When we deal with the set of all integers, Z, we are already used to the fact that although there is a multiplicative identity, 1, which leaves things unchanged when you multiply with it, unlike the real numbers and the rational numbers, in the integers most numbers do not have a multiplicative inverse. The only integers with multiplicative inverses are 1 and –1, whereas every real number other than zero has a multiplicative inverse.

For Z_n, the situation can lie anywhere between these two extremes. If n is a prime number, then every number in Z_n other than zero does have a multiplicative inverse. For example, in Z₇:

1 × 1 ≡ 1 (mod 7)
2 × 4 ≡ 1 (mod 7)
3 × 5 ≡ 1 (mod 7)

But if n is not prime, then only those numbers coprime with n have multiplicative inverses. For example, in Z₈:

1 × 1 ≡ 1 (mod 8)
3 × 3 ≡ 1 (mod 8)
5 × 5 ≡ 1 (mod 8)
7 × 7 ≡ 1 (mod 8)
But 2, 4, 6 have no multiplicative inverses.

It is not hard to see why a number that is not coprime with n — which is to say, it has a factor f greater than 1 in common with n — cannot have a multiplicative inverse in Z_n. If x is divisible by f then any multiple of x, say mx, will also be divisible by f, even when the product is greater than or equal to n and we subtract a multiple of n to keep the result in Z_n. But 1 plus any multiple of n is obviously not divisible by f, so mx can never be equivalent to 1.

Now, consider the subset of Z_n consisting of all elements coprime with n. We will call this Z_n^×.

Clearly 1 is in Z_n^×. If x and y are both in Z_n^×, can xy have a factor greater than 1 in common with n, say f? If it did, then any prime factor p of f would need to divide at least one of x and y, and would also divide n, contradicting our assumption. So, xy will also be in Z_n^×.

Furthermore, suppose x, y and z are all in Z_n^×, and xy ≡ xz (mod n). It follows that:

x (y – z) ≡ 0 (mod n)

In other words, n divides x (y – z). But since x and n have no factors greater than 1 in common, n must divide y – z. So we can conclude that:

For x, y and z in Z_n^×
xy ≡ xz (mod n) if and only if y ≡ z (mod n)

It then follows that if we multiply every element of Z_n^× by some x in Z_n^×, the products must all be distinct, and must be all the elements of Z_n^× itself, including 1. Since one of the products is 1, whatever we multiplied by x to produce 1 will be the unique multiplicative inverse of x.

Taken together, all the properties we have established for Z_n^× (along with the obvious fact that multiplication is associative) make it a commutative group, known as the multiplicative group of integers modulo n.

If n is prime, Z_n^× contains all the non-zero elements of Z_n, so every non-zero element of Z_n has a multiplicative inverse, as we claimed earlier. This means Z_n is an algebraic structure known as a field, like the real numbers.

When n is not prime, Z_n is a commutative ring with unity, which is the same kind of structure as the set of all integers, Z.

When n is prime, the size of Z_n^×, which we will write as |Z_n^×|, is just n–1. But in general, |Z_n^×| is given by Euler’s totient function, φ(n), which counts the numbers less than n that are coprime with n. Euler’s totient function can be evaluated directly, without checking all the numbers for this property individually, with the formula:

φ(n) = n Π_{Distinct primes p that divide n} (1 – 1/p)

Here Π is the symbol for a product, i.e. we are multiplying together the expression that follows, for each distinct prime p that divides n.

It was proved by Gauss that if and only if n is 1, 2, 4, p^k or 2 p^k, for p an odd prime, Z_n^× is a cyclic group, i.e. a group where every element is some integer power of a single element, known as the generator of the group.

Base and Divisor are Coprime

Suppose we compute the digits in the base b representation of the reciprocal of some integer d that is coprime with b, i.e. they share no common factors greater than 1. Then b will belong to the group Z_d^×, as will all its integer powers. For example, if d=13 and b=10, as we saw earlier the powers of 10 (mod 13), starting from 10⁰, are {1, 10, 9, 12, 3, 4}. Note that in this case, since d is prime, we know immediately that |Z_d^×|=12, and it is no coincidence that the size of the set of powers of 10, which is 6, divides |Z_d^×|. The powers of 10 (mod 13) form a subgroup of the group Z_d^×, and the number of elements of any subgroup of a group must divide the number of elements of the group. In general, if d is coprime with b, the length of the reptend of 1/d must divide |Z_d^×| = φ(d).

Given the powers of 10 (mod 13), and knowing the representation for 1/13 in base 10, we can immediately write down the representations for six different fractions with 13 in the denominator. We just take the successive powers of 10 (mod 13) as the numerators, and rotate the digits in the reptend:

We can obtain the representations of the remaining six fractions by doubling the powers of 10 (mod 13) we use as the numerators:

2 × {1, 10, 9, 12, 3, 4} ≡ {2, 7, 5, 11, 6, 8} (mod 13)

and doubling the reptend for 1/13 to obtain the six digits for 2/13, then rotating them as before:

In general, if d is coprime with b, then the powers of b will form a subgroup of Z_d^×, the subgroup generated by b, which can be written more succinctly as <b>. The size of <b> is called the multiplicative order of b modulo d. Either this subgroup <b> will be the entire group Z_d^×, and all fractions less than 1 with d in the denominator when written in lowest terms can be found by cycling the digits of the reptend, or it will comprise some smaller portion of Z_d^×, and the other fractions can be found by taking suitable multiples of <b>, producing reptends with different digits but the same length.

If d is prime, that will cover all the fractions 1/d, 2/d, ..., (d–1)/d. If d is composite, there will be some numerators in that list that are not coprime with d (and hence not in Z_d^×), so d will no longer be the denominator when the fraction is written in lowest terms. For those cases, the representation can be found by examining the numerator and denominator after cancelling any common factors.

Base and Divisor have Common Factors

If the base b and the divisor d have any common factors, we can list all the primes that divide both b and d, and call them p₁, ..., p_m. Define:

h = p₁^k₁ × ... × p_m^k_m

where each k_i is the maximum power of p_i that divides d. It follows that d/h will be an integer coprime with b.

Similarly, define q_i as the maximum power of p_i that divides b. Then define K as the maximum of all the integers ceiling(k_i / q_i), for i = 1, ..., m. Then for each i, the factor of p_i in b^K will be greater than or equal to k_i, and so b^K will be divisible by h.

We can then write:

1/d = (1/b^K) [(b^K/h) / (d/h)]

where the numerator and denominator of the fraction in the square brackets are both integers, and the denominator is coprime with b.

For example, if b = 10 and d = 28, they only have a single prime factor in common:

p₁ = 2
k₁ = 2
h = p₁^k₁ = 4
q₁ = 1
ceiling(k₁ / q₁) = 2
K = 2

1/28 = (1/10²) [(10²/4) / (28/4)]
= (1/10²) [25 / 7]
= (1/100) [3 + 4/7]
= 0.03(571428) ...

So we have reduced the problem of finding the representation of 1/28 to one of finding the representation of 4/7, with a denominator coprime with the base, shifted right by two places, with a prefix of 0.03 before it.

• Symmetries and the 24-cell | Average Shadows | Ball Bearings in a Hypersphere | Black Hole Passing | Born Rigid Motion | Catacaustics | Resonant Modes of a Conical Cavity | The Doppler Shift Triangle Law | Conic Section Orbits | Double-Crossing Orbits | Dihedral Angles | The Ellipse and the Atom | Find The Fake Coin | The Finite Fall | General Relativity in 2+1 dimensions | Howell’s Moving Orbits | Klein's Quartic Curve | Paparazzo vs Bodyguards | Light Mill applet | Littlewood applet | LRL made easy | The Mermin-Peres Magic Square Game | There Are No Corkscrew Orbits | Peeling the Octonions | Ordered Sums | Optimised Origami | Pick Two Points | Weak-field GR near a planar mass | Polar Orbits Around Binary Stars | Planes, Spheres and Pseudospheres | Reptends and Reciprocals | The Rindler Horizon | Rotating Elastic Rings, Disks and Hoops | Constant Weight Rollercoasters | Steffen’s Polyhedron | Superpermutations | Symmetric Waves | Symplectic applet | The Tell-Tale Board | Exact values of regular 10j symbols
• Science Notes
• Back to home page | Site Map | Side-bar Site Map