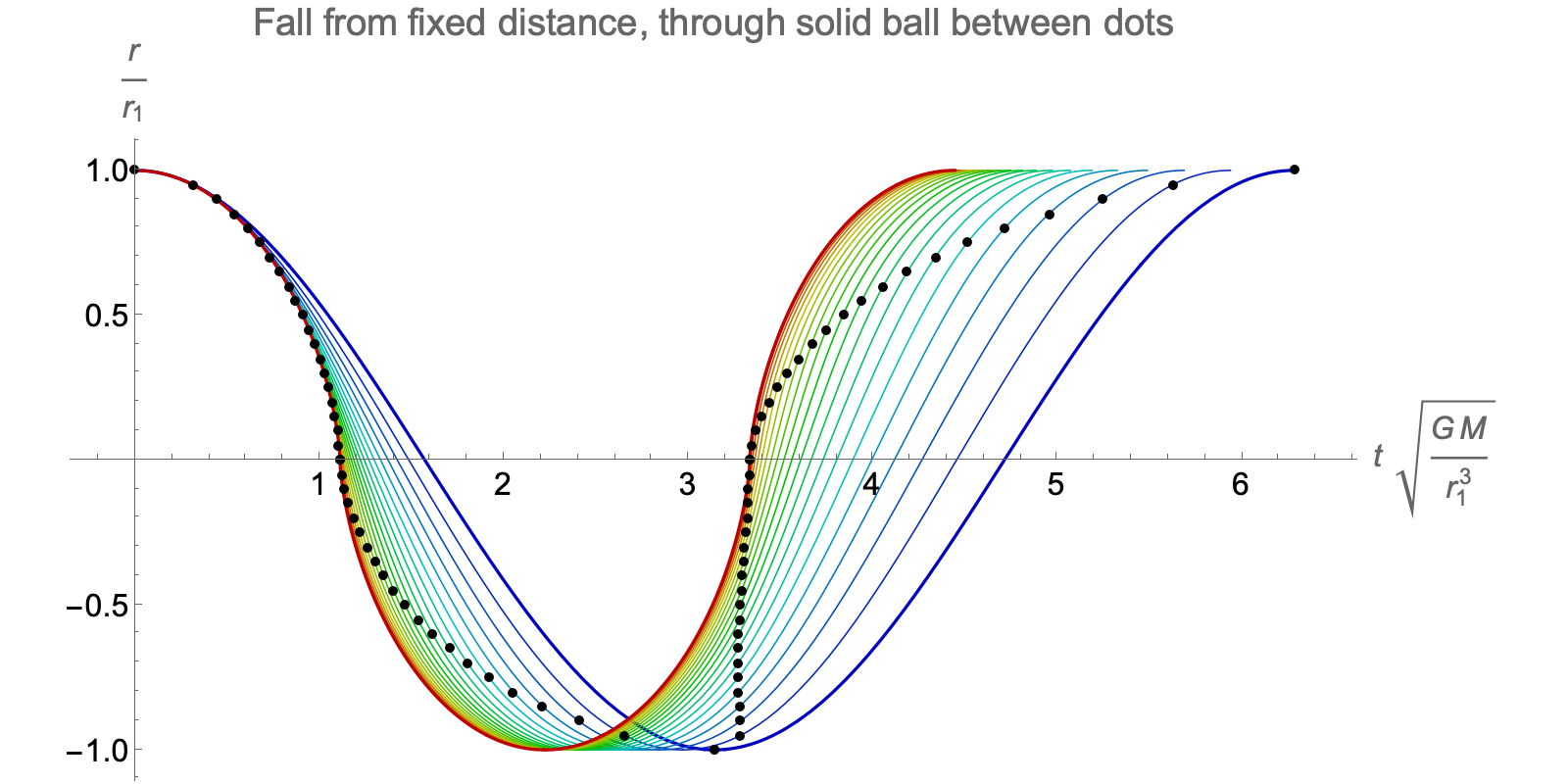
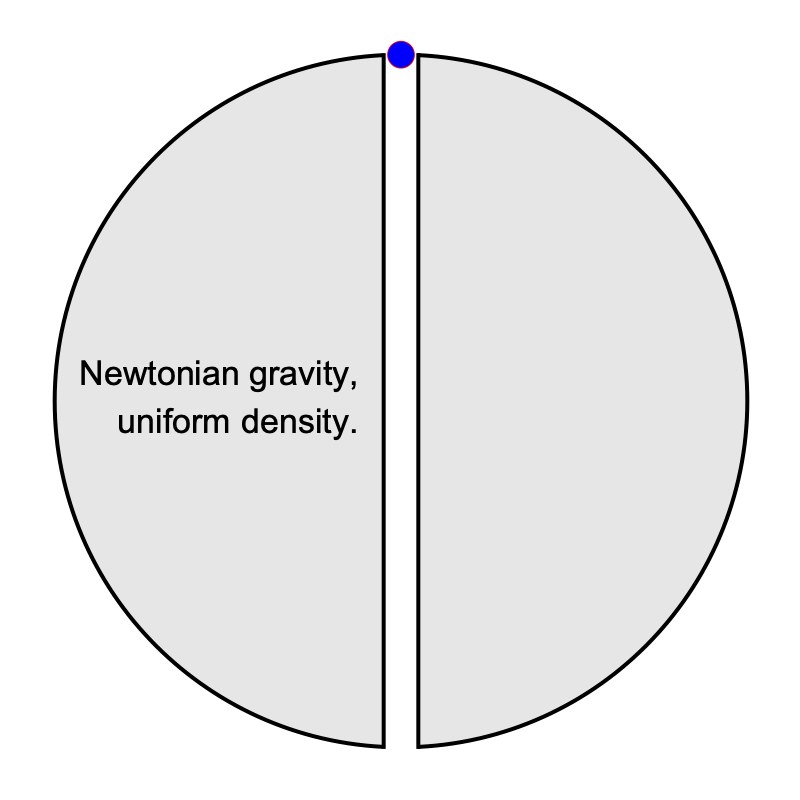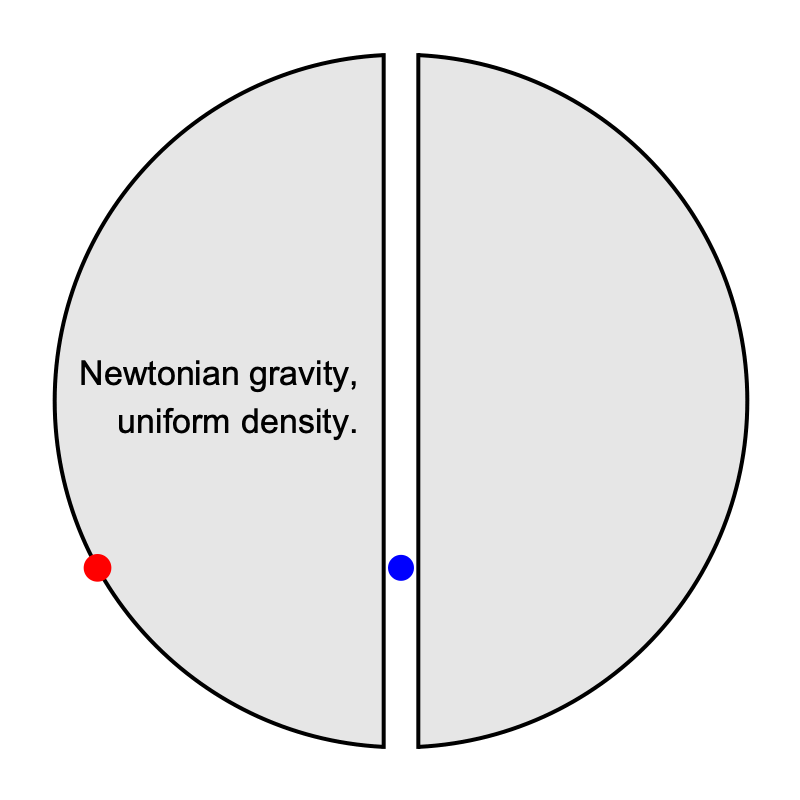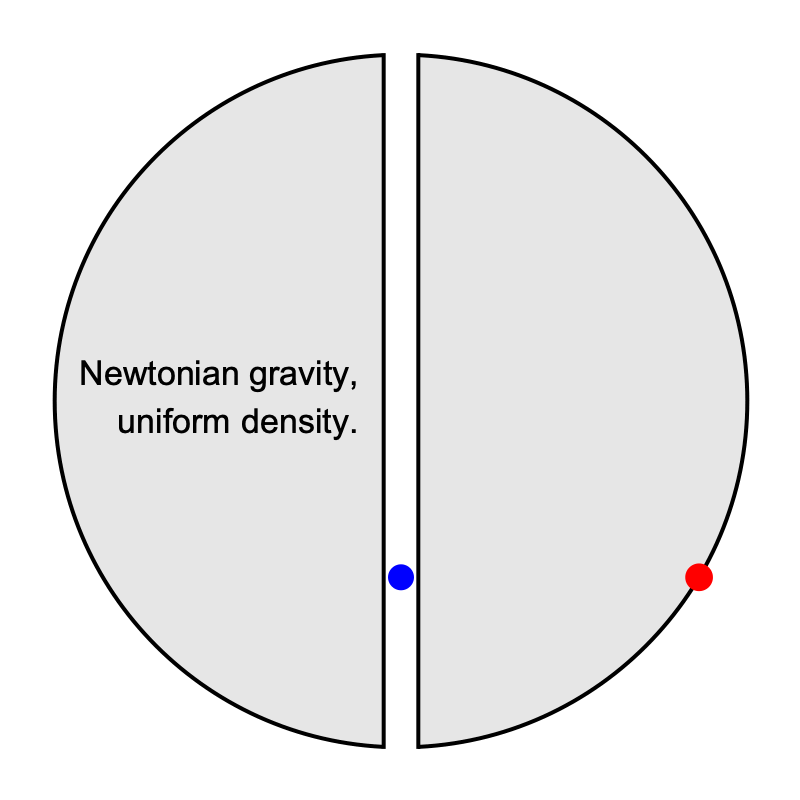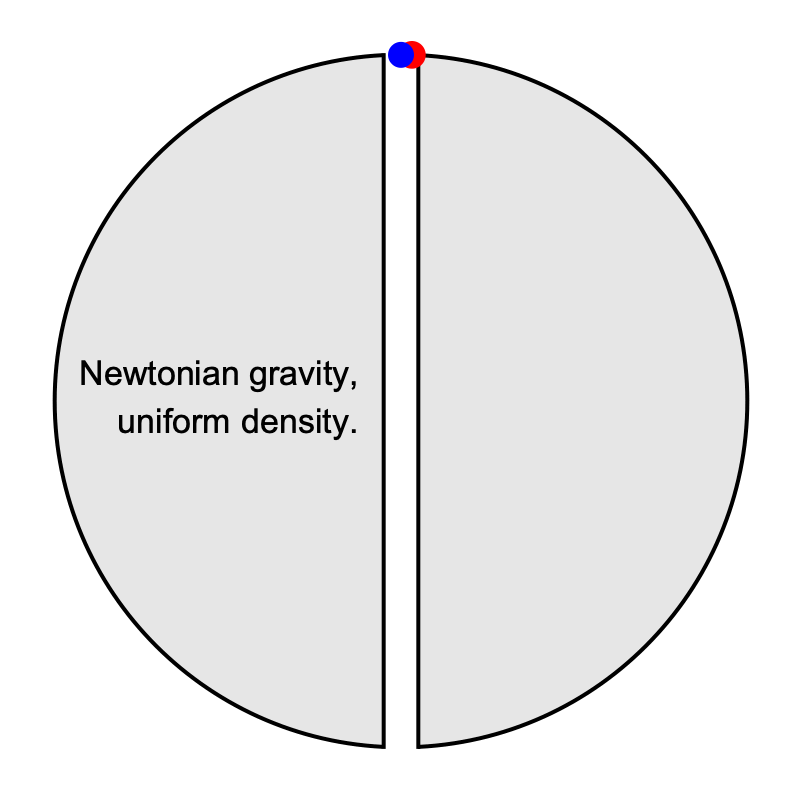
There is a simple thought experiment in Newtonian gravity: drill a thin radial borehole all the way through a solid ball of uniform density, and drop a test particle into the hole, starting from rest at the very top. What happens?
The result is that the particle (blue, in the image on the left) falls all the way through the borehole, comes to a halt at the opposite end, then falls back, undergoing simple harmonic motion (the same kind of motion as an idealised version of a weight bouncing on the end of a spring) with exactly the same period as another test particle (red) orbiting the ball in a circular orbit that grazes the surface.
On this page, we will start by proving that result, but then we will also look at radial motion in the vacuum around the ball in Newtonian gravity, and examine how these systems work in General Relativity — featuring the famous Schwarzschild solution, but starring its much less famous cousin, the second Schwarzschild solution!
A solid ball of radius r and uniform density ρ has mass:
m(r) = (4/3) π ρ r3
In Newtonian physics, the acceleration due to gravity from any spherically symmetrical arrangement of matter is directed towards the centre of symmetry, and it is the same as if all the matter that lies closer to the centre than the point where we are computing the acceleration was concentrated at the centre. (This result is known as the shell theorem, and it was proved by Newton himself.) So, anywhere inside our solid ball, the radial acceleration of a test particle is given by:
r''(t) = –G m(r(t)) / r(t)2
= –(4/3) G π ρ r(t)3 / r(t)2
= –(4/3) G π ρ r(t)
This is the same kind of equation as the one that governs a weight on a spring, where an object experiences a “restoring force” proportional to its displacement from some point. If the particle starts from rest at r = R at time t = 0, the solution is:
rsolid(t) = R cos(ω t)
where ω2 = (4/3) G π ρ
This is easily checked by taking the derivative of the claimed solution twice with respect to time.
How does this compare to the motion of a test particle orbiting a ball of radius R in a grazing circular orbit? If we equate the centrifugal acceleration for circular motion, ω2 R for a circle of radius R and an angular velocity of ω, with the inverse-square acceleration due to gravity, we have:
ω2 R = G m(R) / R2
ω2 = G m(R) / R3
= (4/3) G π ρ
So the angular velocity, and hence the period, is the same for the two kinds of motion.
We have shown that a test particle moving radially inside a ball of uniform density undergoes simple harmonic motion. But what about radial motion through the vacuum around such a ball?
If a test particle with unit mass starts from rest at some radius r1 which is greater than the radius of the ball, R, we can find its kinetic energy K at any other r outside the ball from the change in its potential energy, U:
K(r) = ½ v(r)2
= U(r1) – U(r)
= G M (1/r – 1/r1)
where we are writing M for the total mass of the ball, m(R).
This is equivalent to:
dt/dr = 1/v(r) = ±1 / √[2 G M (1/r – 1/r1)]
The solution to this equation, for the particle starting its fall at time t = 0, is:
tvac(r) = √[r13/(2 G M)] (acos(√[r/r1]) + √[(r/r1)(1 – r/r1)])
We can compare this with the function giving time to reach a given radius for motion entirely through the solid ball:
tsolid(r) = √[R3/(G M)] acos(r/R)
In the limit where the ball is replaced by a point mass, the time for the test particle to fall down to r = 0 is:
tvac(0) = (π/2) √[r13/(2 G M)]
compared to:
tsolid(0) = (π/2) √[R3/(G M)]
This shows that the fall through the vacuum would be faster, which makes sense because the test particle feels the full force of all the mass throughout its motion, whereas inside the ball the amount of mass attracting it grows steadily smaller.
It is worth pointing out that the limiting case of a radial fall through the vacuum down to a point mass can be continued beyond r = 0 in two different ways. If we think of it as the limit of a series of ever skinnier elliptical orbits with the mass at one focus of the ellipse, in each case the test particle, at its closest approach, swings around the mass and reverses direction ever more rapidly. In that scenario, the fall down to r = 0 is half of a complete orbit, for an elliptical orbit whose semi-major axis a is half the starting radius, i.e. a = ½r1. The orbital period T for a test mass in an elliptical orbit depends only on the orbit’s semi-major axis and the mass of the attracting body:
T(a, M) = 2 π √[a3 / (G M)]
which give us, for half the orbital period of an orbit with a = ½r1:
½T(½r1, M) = (π/2) √[r13/(2 G M)]
in agreement with the value we found for tvac(0).
This is in contrast with the scenario where we drop a test particle from the top of a radial borehole through a ball of uniform mass, but then fix the point where we drop the particle, while shrinking the ball and increasing its density to keep its mass constant. In that case, rather than swinging around the ball, the test particle always falls right through it. The time it takes to fall to r = 0 approaches the same limit, but when the acceleration becomes infinite the infalling solution continues as an ascending solution on the opposite side of the mass, rather than on the same side.

The plot above shows one cycle for various cases of the motion where a test particle falls from the same starting radius, r1, and passes through a borehole in a solid ball of the same mass, M, but different radii, R. The dots on each curve mark the extent of the solid ball. The slowest cycle takes place entirely within the ball, while the fastest is the limiting case where the ball has shrunk to a radius of zero but the test particle still “falls through it” rather than swinging around it.
In 1916, shortly before his death, the German physicist and astronomer Karl Schwarzschild published two papers that described exact solutions of Einstein’s equations for the geometry of space-time. The first solution is for the gravitational field due to a point mass[1], and this Schwarzschild solution is famous for describing the space-time geometry that we now understand to be that of a [non-rotating, electrically neutral] black hole. It also describes the vacuum surrounding any [non-rotating, electrically neutral] spherically symmetrical mass.
The second Schwarzschild solution is for the gravitational field due to a ball of incompressible fluid[2], or in other words a ball of uniform density, since an incompressible fluid does not change its density under pressure. So, this is the General Relativistic equivalent of the Newtonian solid ball of uniform density that we considered in the previous section.
The two Schwarzschild metrics, for a ball of total mass M and coordinate radius R, are given by[3]:
ds2 = –(1–2M/r) dt2 + dr2 / (1–2M/r) + r2 (dθ2 + sin2θ dφ2) r > R ds2 = –¼(3 √[1–2M/R] – √[1–2Mr2/R3])2 dt2 + dr2 / (1–2Mr2/R3) + r2 (dθ2 + sin2θ dφ2) r ≤ R
Here we are following common practice in General Relativity and using geometric units, which are chosen to make the gravitational constant G and the speed of light c both equal to 1. In these units, times and masses are measured in the same units as distances. A time in conventional units is multiplied by c ≈ 2.998×108 metres/sec to convert it to a distance, and a mass is multiplied by G/c2 ≈ 7.425×10–28 metres/kg (or about 1,483 metres per solar mass).
The Schwarzschild r coordinate is chosen to make the surface area of a sphere of coordinate radius r equal to 4πr2, so the coordinates θ and φ for a given value of r act like ordinary spherical polar coordinates. The Schwarzschild t coordinate is chosen so that all slices of space-time with a fixed t coordinate have a geometry that is independent of t, as can be seen by the fact that t itself does not appear in the metric.
We won’t describe in detail how these metrics are derived, but it comes down to taking a generic, spherically symmetric metric that is unchanging in time:
| ds2 | = | –P(r) dt2 + Q(r) dr2 + r2 (dθ2 + sin2θ dφ2) |
and computing the Einstein tensor, derived from this metric, which quantifies certain aspects of space-time curvature. Einstein’s equation then tells us that this tensor is proportional to the stress-energy tensor, which has components that describe the density of mass-energy and the pressure of whatever matter is responsible for the space-time curvature.
Setting the density to zero gives us a differential equation for Q(r), and once we solve that, and substitute the solution into expressions for the pressure in the radial and tangential directions, setting either of them to zero yields the same solution for P(r). These solutions for P(r) and Q(r) give us the first Schwarzschild metric, which applies to the vacuum outside the ball.
Setting the density to a non-zero constant value, ρ, gives us a different solution for Q(r), and then we obtain P(r) by requiring the pressure to be the same in the radial and tangential directions. That gives us the second Schwarzschild metric. It also gives us an explicit formula for the pressure inside the ball as a function of r:
p(r) = ρ (α(r) – α(R)) / (3α(R) – α(r))
where α(r) = √[1–2Mr2/R3]
The wonderful thing about Einstein’s equation is that the pressure we obtain this way will automatically be precisely what is needed to balance the gravitational attraction at each point inside the ball; we don’t need to perform a separate computation in relativistic hydrostatics to make this come out right. The Einstein tensor, by construction, has the geometric property of being “divergence free” that, when shared by the stress-energy tensor guarantees that it has the correct physical properties.
The pressure at the surface of the ball, r = R, is always zero. If we fix the mass of the ball but make it smaller, the pressure at the centre, r = 0, increases, and becomes infinite when R = (9/4)M. That is slightly more than r = 2M, which marks the event horizon of an existing black hole, and which guarantees that a black hole will form if a mass of M is squeezed down to within that radius. Although our uniform-density ball is a physically unrealistic toy model (certainly not applicable to stars or planets, though perhaps a fair approximation for a moderately sized, non-rotating globe of pure water), so long as R > (9/4)M the model should not yield infinite values for any physical quantity.
The density, ρ, of mass-energy within the ball doesn’t appear explicitly in the second Schwarzschild metric as we have written it, but it is related to the parameters M and R by the formula:
M = (4/3) π ρ R3
This might seem a bit strange, given that the volume of the ball with an r coordinate ranging from 0 to R is larger than (4/3) π R3, the volume of a ball in Euclidean space with radius R, because the metric tells us that ds/dr is greater than 1. Surely M should be greater than the value given above, reflecting that greater volume?
To understand what is happening here, imagine we assemble the ball by dropping in material from a large distance (we will say “from infinity”, which really just means from a large enough distance that we can neglect the gravitational effects of the ball there). As it falls, the material will gain kinetic energy, so its mass-energy will increase compared to the original value. So we can spread it out across a larger volume than it would have occupied “at infinity”, while keeping its density constant at ρ. The mass M measures the total mass-energy that we have dropped onto the ball “from infinity”, and it is the appropriate way to quantify the gravitational field of the ball, inasmuch as the angular velocity ω(r) of a test particle in a circular orbit around the ball at a radius of r will obey the asymptotic relationship (in our units where G = 1):
limitr→∞ω2(r) r3 = M
To analyse the orbits of interest to us, we will start with the fact that the world line of a free-falling test particle, moving only under the influence of gravity, will be a geodesic in the space-time geometry. We will use the symbol u to denote its 4-velocity: the unit vector tangent to its world line. The components of the vector u in our coordinate system are simply the rate of change with proper time τ, along the geodesic, of the coordinates:
ut = ∂τ t
ur = ∂τ r
uφ = ∂τ φ
uθ = ∂τ θ
Because the geometry is spherically symmetrical, we can always choose coordinates so that the world line of the test particle lies in the “equatorial plane” at θ=π/2, and uθ = ∂τ θ = 0.
Since the metric is independent of the coordinates t and φ, the coordinate vector fields ∂t and ∂φ are Killing vector fields: fields that describe ways of “sliding” a figure through the geometry while preserving its shape and size, in the same way that we can imagine, say, adding 5 degrees to the longitude of every point on an island without distorting its geography. (For an informal discussion of Killing vector fields, try this page; though it starts with a quote from my novel Incandescence, it doesn’t actually require any familiarity with that book.)
A consequence of ∂t and ∂φ being Killing vector fields is that the dot product of the tangent to any geodesic with these fields will remain constant along the length of the geodesic. So for the entire world line of our test particle, we will have:
u · ∂t = ut gtt = –E
u · ∂φ = uφ gφφ = L
where gtt and gφφ are the coefficients of dt2 and dφ2 in the metric, and we’ve introduced E and L as names for the two constants, since they measure the energy and angular momentum, per unit rest mass, of the particle. The fact that u is a unit vector means:
gtt (ut)2 + grr (ur)2 + gφφ (uφ)2 = –1
(∂τ r)2 = (ur)2 = [–gtt (ut)2 –gφφ (uφ)2 – 1] / grr
= [–E2/gtt – L2/gφφ – 1] / grr
For the first Schwarzschild metric, this becomes:
(∂τ r)2 = E2 + (1–2M/r) [ – L2/r2 – 1]
= E2 – (r – 2M) (L2 + r2) / r3
This formula lets us think of the radial motion of the test particle as if it was moving in a kind of potential-energy well, given by:
V(r) = (r – 2M) (L2 + r2) / r3
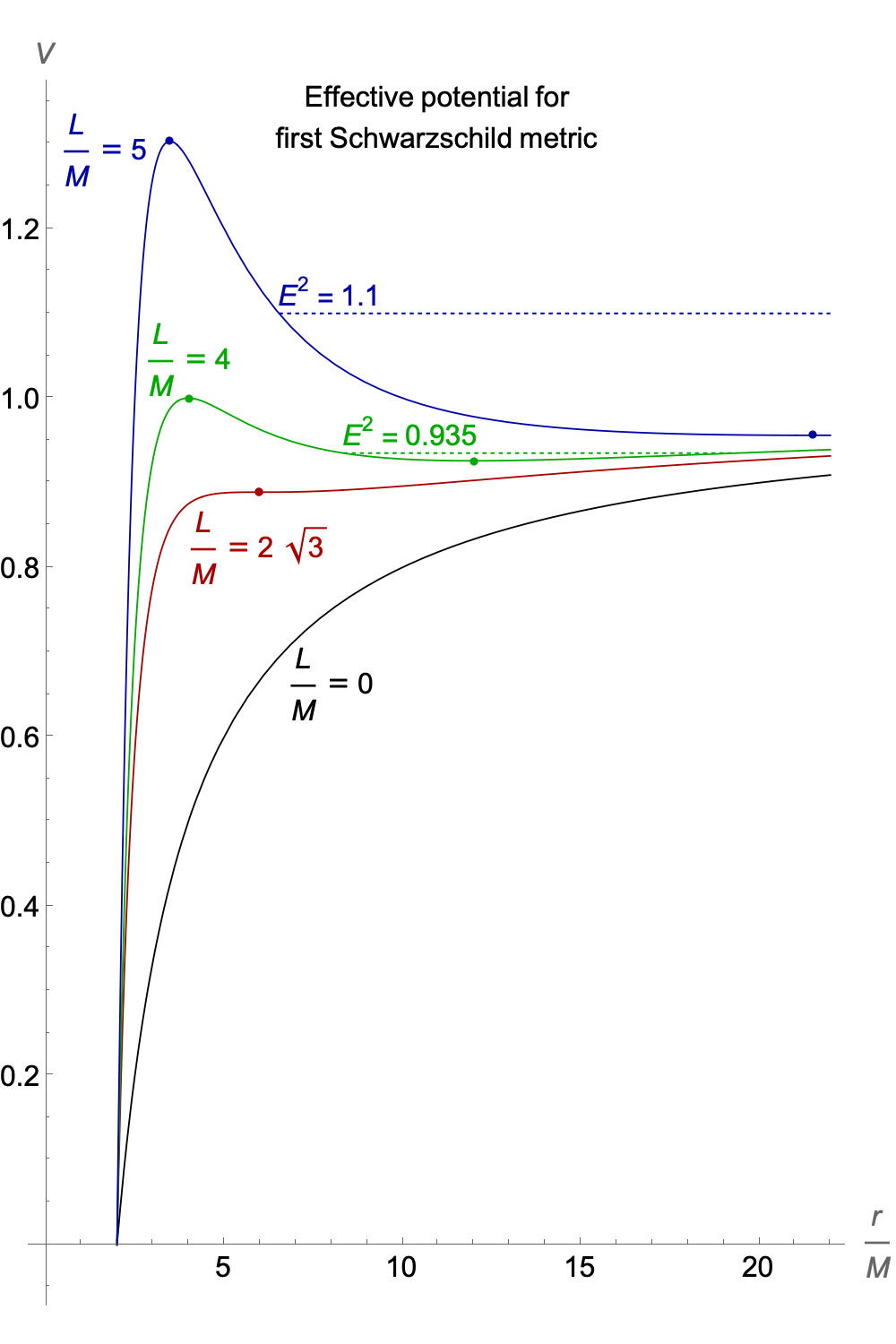
The squared energy E2 needs to be greater than or equal to V(r), since (∂τ r)2 cannot be negative, so for a given value of E and L this will prescribe the range of r values where the particle can be. Whenever E2 = V(r) the radial velocity must be zero, which marks points where the particle changes from incoming to outgoing.
For example, in the diagram on the left, for L/M = 5 (which gives the blue curve for V(r)) and E2 = 1.1 (the dashed blue line), the particle will approach from infinity, reach a minimum r/M of about 6.5, then move away again, in an unbound orbit. An orbit like this would be hyperbolic in Newtonian gravity, but takes on a sightly different shape in the relativistic version.
For L/M = 4 (which gives the green curve for V(r)) and E2 = 0.935 (the dashed green line), the particle moves between a minimum r/M of about 8.3 and a maximum of 19.4, in a bound orbit. This kind of orbit would be elliptical in Newtonian gravity, but in the relativistic version it does not form a closed curve, because the angular and radial motion will not have precisely the same periods.
The dots on the curves mark local maxima and minima for V(r). Stable circular orbits can take place at the minima, which can only occur at r > 6M. For 3M < r < 6M, the potential can have a maximum, and in principle there could be a circular orbit there, but it will be unstable.
For L/M = 2√3 the maxima and minima merge at r = 6M, and for L/M < 2√3 there are no maxima or minima and the particle will always fall into the singularity at r = 0.
We can compute the radial acceleration, the second derivative of r with respect to proper time τ:
(∂τ r)2 = E2 – V(r)
2 (∂τ r) (∂τ, τ r) = –V '(r) (∂τ r)
∂τ, τ r = –½V '(r)
= –M/r2 + L2 (r – 3M) / r4
So we have the ordinary inverse-square acceleration that is familiar from Newtonian gravity, plus a centrifugal acceleration that changes sign at r = 3M. That change of sign makes circular orbits in the first Schwarzschild metric impossible for r ≤ 3M, because the centrifugal acceleration points inwards and there is nothing to balance the gravitational attraction. (No object with rest mass can orbit at precisely 3M, but in principle a photon can orbit at that radius. Analysing photon geodesics around black holes is beyond the scope of this page, but you can read a bit about them here.)
Now, suppose we have a test particle in a circular orbit with coordinate radius R. If we set the radial acceleration to zero and solve for L, we find:
L = ±R √[M / (R – 3M)]
If we substitute this into V(r), set the radial velocity to zero, and solve for E, we get:
E = (R – 2M) / √[R (R – 3M)]
The angular velocity of the circular orbit with respect to proper time τ, is:
ωτ(R) = uφ = L / gφφ = L / R2
= √[M / (R – 3M)] / R
If we want to convert this to coordinate time, t, we need:
dt/dτ = ut = –E / gtt
= √[R / (R – 3M)]
So the angular velocity with respect to coordinate time is:
ωt(R) = ωτ(R) / (dt/dτ)
= √[M / (R – 3M)] √[(R – 3M) / R] / R
= √[M / R3]
This is the same formula as for the angular velocity of a Newtonian circular orbit, although of course coordinate time t is not the proper time either for the orbiting particle or for a stationary bystander at the same radial position.
What about radial motion in the first Schwarzschild metric? If we set L = 0, we have:
(∂τ r)2 = E2 – (1–2M/r)
If the particle is at rest when r = r1, we have:
E2 = 1–2M/r1
So the radial motion is given by:
(∂τ r)2 = 1–2M/r1 – (1–2M/r)
= 2M (1/r – 1/r1)
dτ/dr = ±1 / √[2M (1/r – 1/r1)]
Apart from the factor of G that we have set to 1, this is precisely the same as the equation we found for dt/dr in the Newtonian case! So the solution takes the same form:
Proper time for radial fall from r1 to r
τvac(r1, r) = √[r13/(2 M)] (acos(√[r/r1]) + √[(r/r1)(1 – r/r1)])
If the first Schwarzschild metric applies down to r = 2M or less then we are describing a black hole, so we can’t talk about the limiting case of a radial oscillator where the particle moves through vacuum all the way to r = 0 and then ascends on the other side, as we did for the Newtonian version. Nevertheless, this formula will tell us the proper time for a particle that falls from r = r1 to any other smaller value of r, including the event horizon at r = 2M and the singularity at r = 0. For the latter:
τvac(0) = (π/2) √[r13/(2 M)]
You can read much more about objects (and people) falling into black holes, what they look like from afar, and when they can and can’t be rescued, in the page I wrote on The Finite Fall.
If we want to compute the coordinate time for radial motion, we have:
dt/dr = (dt/dτ) (dτ/dr)
= ±(–E/gtt) / √[2M (1 / r – 1 / r1)]
= ±(√[1–2M/r1] / (1–2M/r)) / √[2M (1/r – 1/r1)]
The integral of this, assuming we are descending from r1 at t = 0 to some r > 2M, is:
Coordinate time for radial fall from r1 to r
tvac(r1, r) = √[r1/(2M) – 1] (√[r (r1 – r)] + (4M + r1) acos(√[r/r1])) + 4M atanh(√[r1/r – 1] / √[r1/(2M) – 1] )
Now, turning to the second Schwarzschild metric, we have:
(∂τ r)2 = [–E2/gtt – L2/gφφ – 1] / grr
= (1–2Mr2/R3) [4 E2/(3 √[1–2M/R] – √[1–2Mr2/R3])2 – L2/r2 – 1]
For our borehole oscillator thought experiment, we have L = 0 for radial motion, and the particle is motionless when r = R. This gives us:
4 E2/(3 √[1–2M/R] – √[1–2M/R])2 – 1 = 0
E2 = 1–2M/R
and the radial motion becomes:
(∂τ r)2 = (1–2Mr2/R3) [4 (1–2M/R)/(3 √[1–2M/R] – √[1–2Mr2/R3])2 – 1]
If we want to work in coordinate time, t, we can use:
dt/dτ = ut = E / gtt
(dτ/dt)2 = (gtt)2 / E2
= (3 √[1–2M/R] – √[1–2Mr2/R3])4 / [16 (1–2M/R)]
(dr/dt)2 = (dτ/dt)2 (∂τ r)2
Integrating the last equation here is a bit complicated, so we will leave the calculations to an appendix.
The upshot is that the coordinate-time angular velocity ωt is slower for the borehole than for a grazing circular orbit. So in the General-Relativistic version of our thought experiment, when the particle in the circular orbit has returned to its original position, the particle that was dropped into the borehole will still be on its way back up.
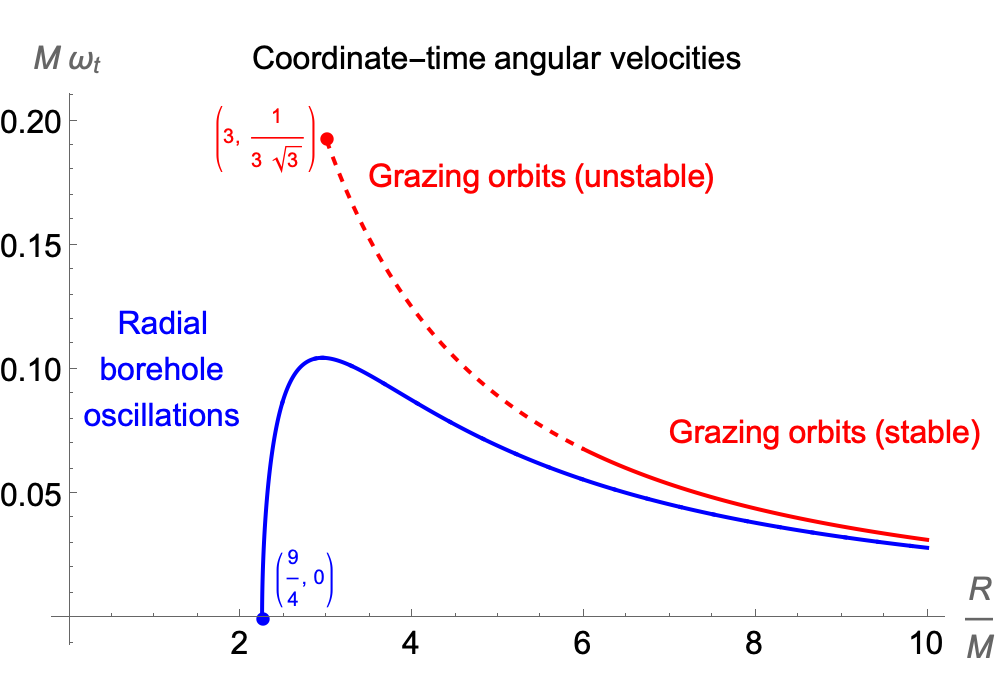
As R approaches the minimum possible value of (9/4)M, which is when the pressure at the centre of the ball would become infinite, the coordinate-time angular velocity for the borehole oscillations approaches zero. In other words, the period becomes arbitrarily long. This is similar to the way that a rocket that passes close to the event horizon of a black hole can take arbitrarily long to return to a distant stationary observer, according to the stationary observer’s clock. But the proper time recorded by a clock on the rocket itself is bounded, and similarly, the proper time recorded by a clock undergoing borehole oscillations is bounded, as we can see from the plot below.
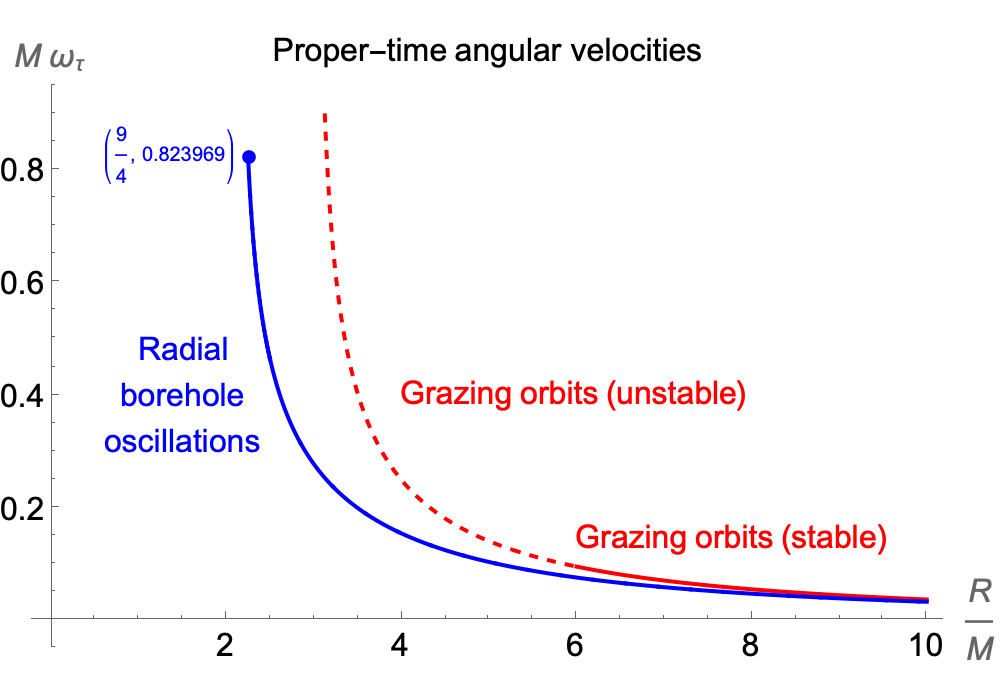
According to a clock oscillating up and down in the borehole, the rate of oscillations increases monotonically as R gets smaller, approaching a finite maximum value as R approaches (9/4)M. The rate is always slower than the proper time rate for a clock in a grazing circular orbit (which approaches infinity as R approaches 3M and the orbital velocity approaches the speed of light).
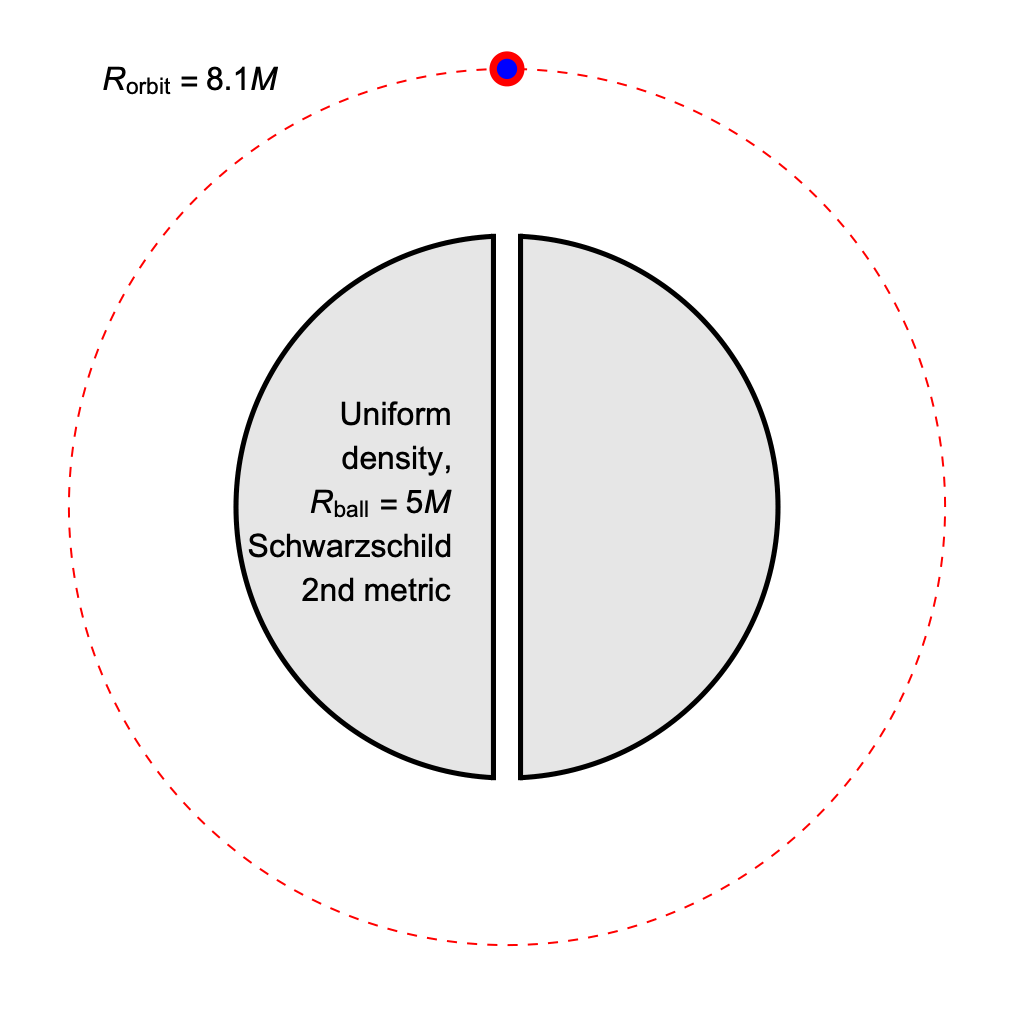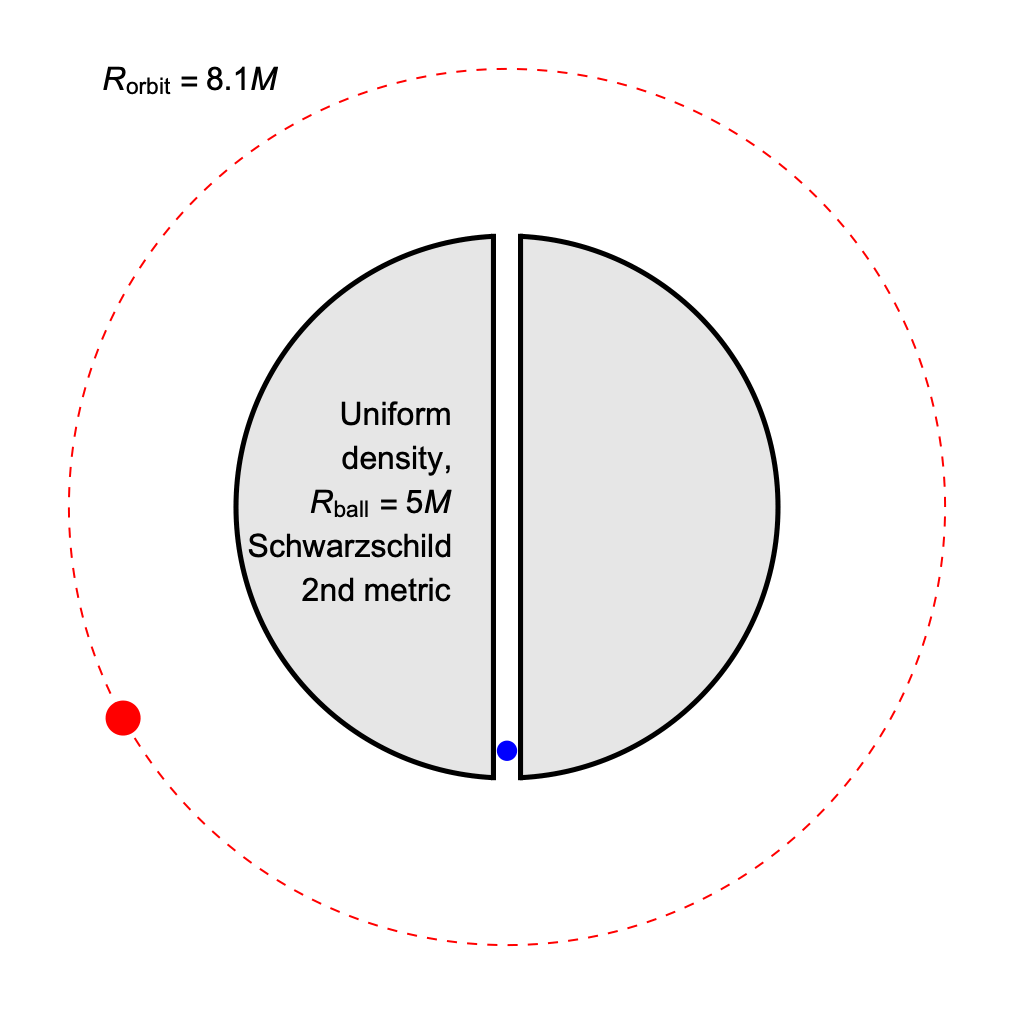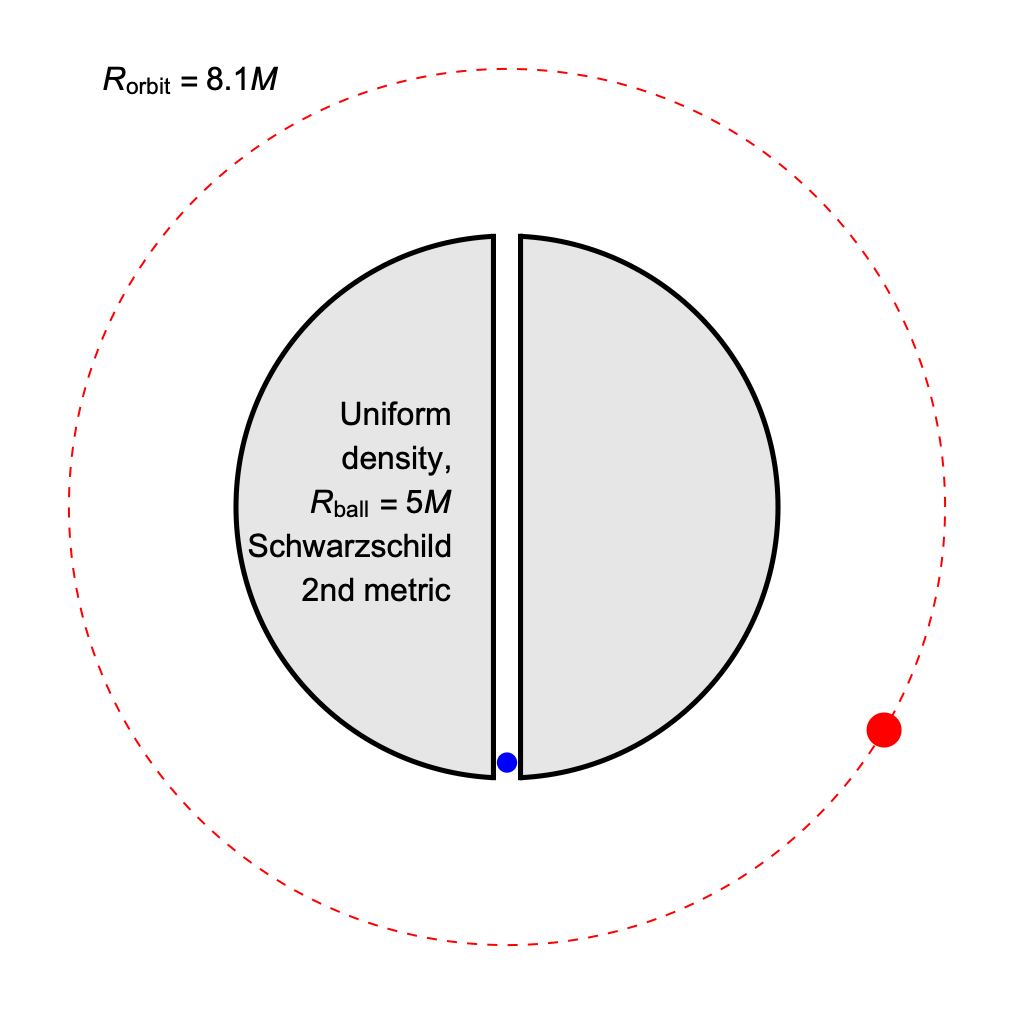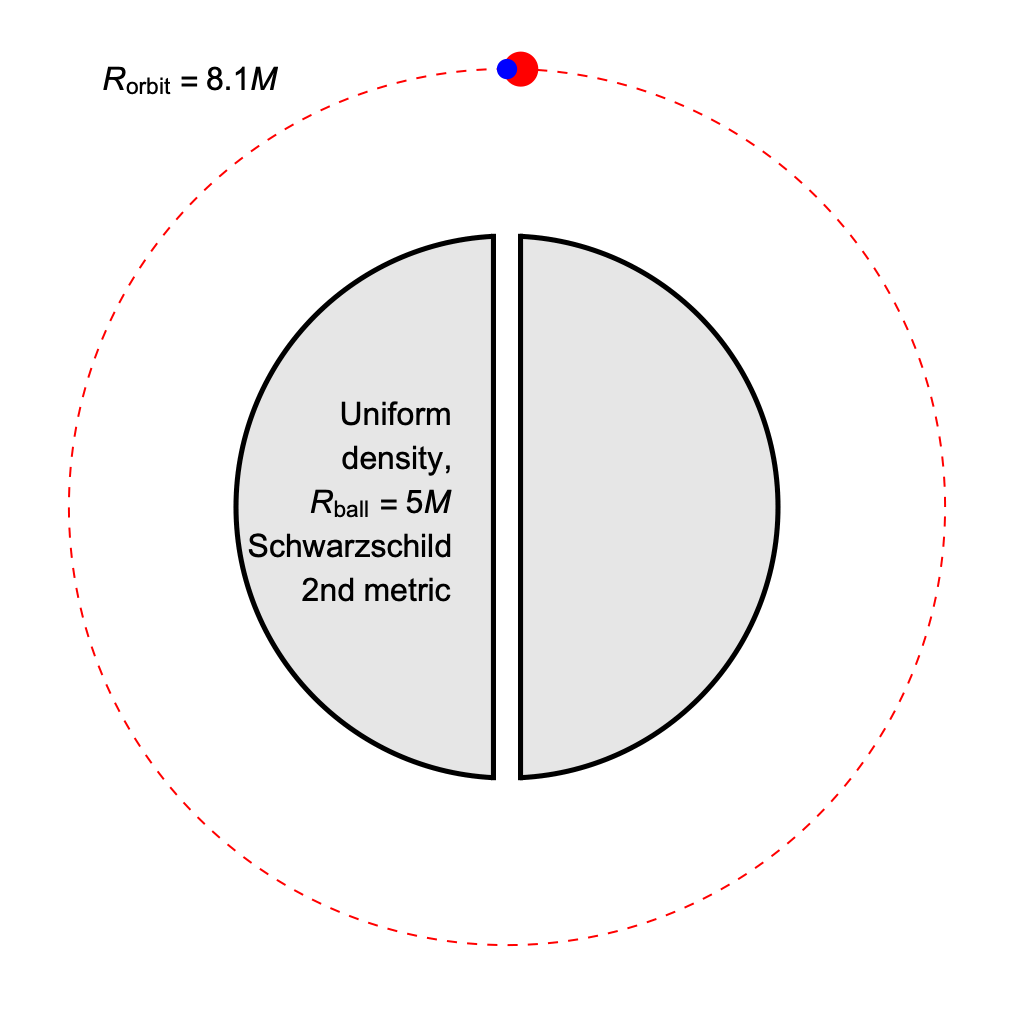
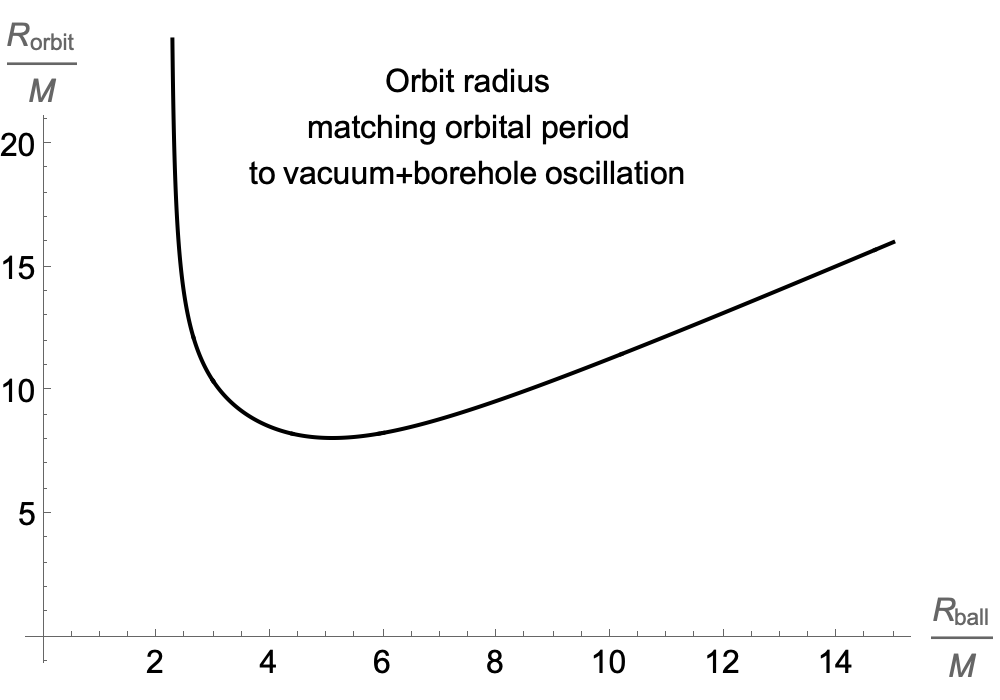
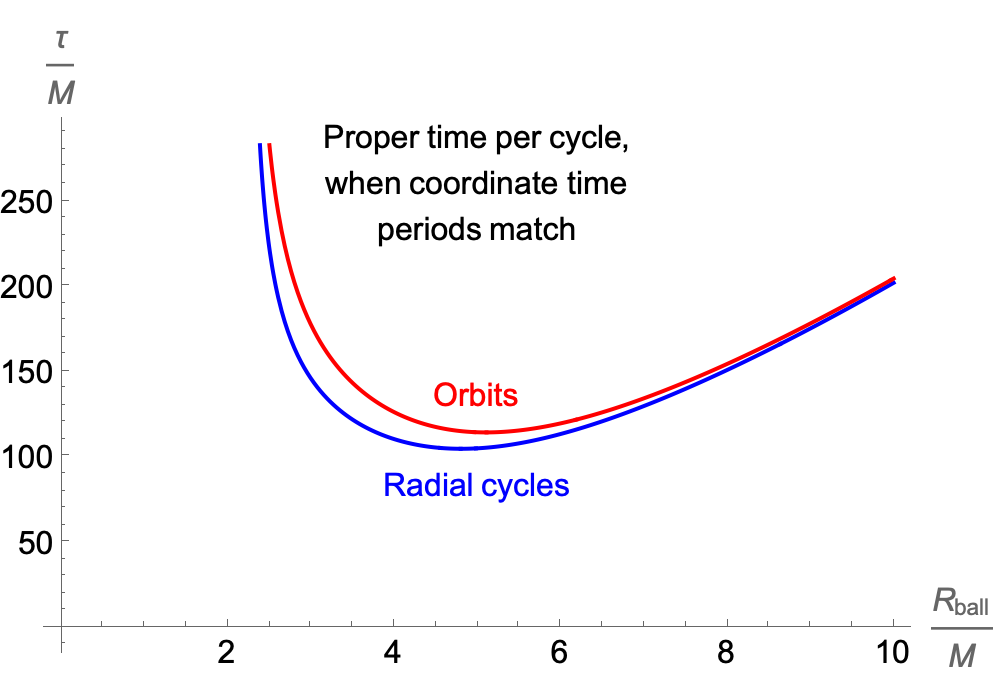
It is possible to match the period of an orbiting body and one undergoing radial oscillations, if we can make the orbital radius larger than the radius of the ball, and allow the radial oscillations to include a fall through vacuum from the same height as the orbit.
The orbital radius at which the coordinate-time periods match is always greater than 6M, so these are physically viable, stable orbits.
The proper time per cycle, as measured by clocks on the orbiting / radially-falling bodies respectively, is always slightly greater for the orbiting clock. This is the opposite of the relationship that holds when the orbit grazes the surface of the ball.
What if we aim a beam of light straight down the borehole?
For light, the ds2 measured by the metric is zero, so light travelling in a purely radial direction in either of the Schwarzschild space-times must obey:
dt/dr = ±√[–grr/gtt]
If we solve this for a beam of light directed towards the centre of the ball, starting from the top of the borehole at t = 0, we get:
tLight(r) = (R2 ξ / M) (atan(ξ) + atan(3ξ) – atan(ξ r/R) – atan(3ξ r √[(R – 2M) / (R3 – 2Mr2)])
where ξ = √[M/(4R–9M)]
tLight(0) = (R2 ξ / M) (atan(ξ) + atan(3ξ))
When R = 3M we have:
ξ = 1/√3
atan(ξ) + atan(3ξ) = π/2
tLight(0) = (π/2) 3√3 M
ωt(R) = √[M / R3]
ωt(3M) = 1/(3√3 M)
So the radius R for the ball such that the orbital quarter-cycle equals the time for light to reach the centre is 3M, the radius where the smallest circular orbit exists — and exists only for photons. For any larger ball, light will cross the borehole faster than any orbiting object can move between the two ends.
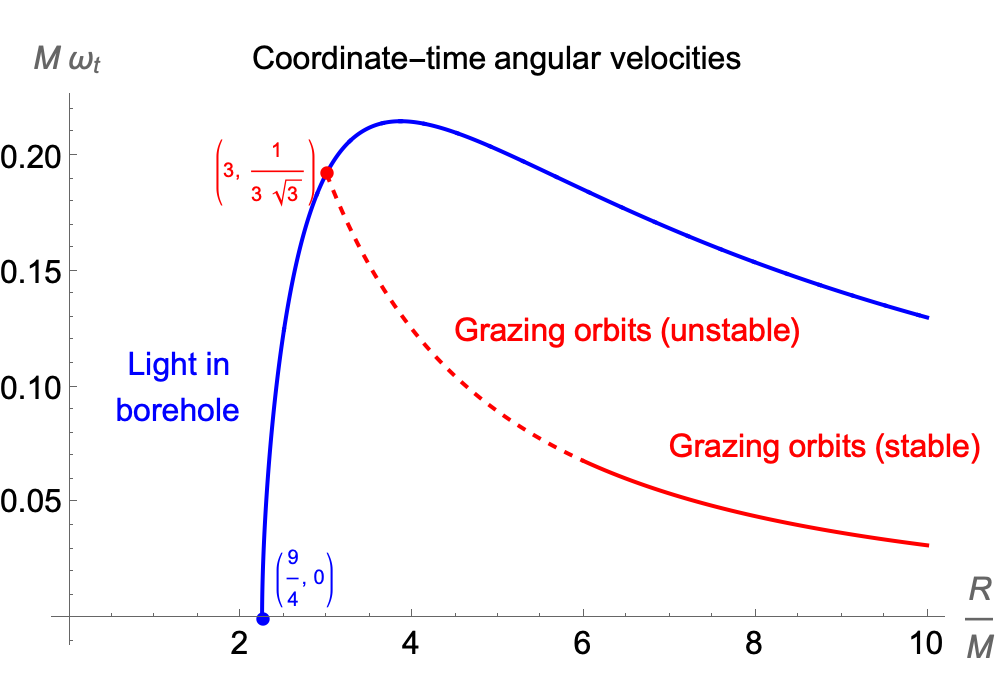
Consider the surface in three-dimensional Euclidean space, parameterised by two coordinates, r and φ, with 0 ≤ r ≤ R:
S2(r, φ) = (r cos(φ), r sin(φ), R (√[R/(2M) – 1] – √[R/(2M) – r2/R2]))
If we compute the squared distance of an arbitrary point on this surface from the point c = (0, 0, R √[R/(2M) – 1]), it turns out to be constant:
|S2(r, φ) – c|2 = r2 + R2 (R/(2M) – r2/R2)
= R3 / (2M)
So our surface S2(r, φ) is part of a sphere, centred on c, with radius √[R3 / (2M)].
Why parameterise a sphere this way? Let’s compute the square of the distance corresponding to a change in the r coordinate:
∂r S2(r, φ) = (cos(φ), sin(φ), r / √[R3/(2M) – r2])
|∂r S2(r, φ)|2 = 1 + r2 / (R3/(2M) – r2)
= 1 / (1–2Mr2/R3)
So, distances within this surface depend on r in exactly the same way as they do in the second Schwarzschild metric!
In other words, this spherical bowl has exactly the same geometry as a slice of curved space cutting through the centre of the ball of uniform density in the second Schwarzschild solution.
We can do the same thing for a slice through the vacuum outside the ball, described by the first Schwarzschild metric:
S1(r, φ) = (r cos(φ), r sin(φ), √[8M] (√[r – 2M] – √[R – 2M]))
∂r S1(r, φ) = (cos(φ), sin(φ), 1 / √[(r/(2M) – 1)]
|∂r S1(r, φ)|2 = 1 + 1 / (r/(2M) – 1)
= 1 / (1–2M/r)
The image below shows a surface with the geometry of a spatial slice through the combined Schwarzschild space-time, for a ball of radius 4M, showing the vacuum geometry (the green surface) out to 6M.

This is fine for visualising the geometry of space alone, but to understand the motion of free-falling objects, we need to look at a slice that includes the time coordinate. We can’t embed a slice like that in ordinary three-dimensional Euclidean space, but we can embed it in a flat space-time with two time-like dimensions and one space-like dimension.
Why two time-like dimensions, when there is only one time-like dimension in the slice itself? We want to be able to bend the surface along its time-like dimension, so we need two such dimensions in the ambient space from which the surface inherits its space-like and time-like geometry.

The image above shows a slice through the radial and time dimensions of the combined Schwarzschild space-time, for a ball of radius 4M, along with the vacuum geometry (the green surface) out to 6M. The red curve drawn on the surface is part of the world line for an object dropped into a radial borehole, and just as the world line is a geodesic in the actual curved space-time, it is a geodesic of this curved surface embedded in a flat space-time.
The time dimension here appears to form a closed loop, but that has nothing to do with the real topology of the Schwarzschild space-time; it just looks nicer if we take one cycle of the borehole oscillations and adjust a free parameter in the embedding so that it wraps around exactly 360 degrees, rather than leaving a gap.
The white surface, corresponding to a t-r slice of the second Schwarzschild space-time, is given by:
H(t, r) = (J(r) cos(a t), J(r) sin(a t), E(asin(Ω r) | –Ω2/(4a2)) / Ω )
Ω = √[2M/R3]
a is a parameter we are free to choose.
E is an incomplete elliptic integral of the second kind.
J(r) = ½(3 √[1–2M/R] – √[1–2Mr2/R3]) / a
A vector pointing along the surface in the t direction lies solely in the first two dimensions of the flat space-time in which the surface is embedded, so by making those two dimensions time-like the t coordinate inherits that property. Specifically:
∂t H(t, r) = (–a J(r) sin(a t), a J(r) cos(a t), 0)
|∂t H(t, r)|2 = –a2 J(r)2
= –¼(3 √[1–2M/R] – √[1–2Mr2/R3])2
which is the coefficient of dt2 in the second Schwarzschild metric. Similarly, the squared length of a vector pointing along the surface in the r direction (which has components in both space-like and time-like directions, so we take the difference of the squared components), is equal to the coefficient of dr2 in the second Schwarzschild metric.
By choosing a appropriately, we can embed a time interval corresponding to one full borehole oscillation so that it wraps around and comes full circle.
For the surrounding vacuum geometry, although the metric is simpler I am not aware of a closed-form solution for the embedding, so it was achieved with numerical integration.
Our aim here is to compute coordinate time, t, as a function of the coordinate radius, r, for a particle that falls from rest at r = R down to the centre of a solid ball of uniform density, with mass M and coordinate radius R, whose space-time geometry is described by the second Schwarzschild metric.
We previously found that:
(∂τ r)2 = (1–2Mr2/R3) [4 (1–2M/R)/(3 √[1–2M/R] – √[1–2Mr2/R3])2 – 1]
(dτ/dt)2 = (3 √[1–2M/R] – √[1–2Mr2/R3])4 / [16 (1–2M/R)]
Since r is the independent variable, we need to integrate:
dt/dr = 1 / [(dτ/dt) (∂τ r)]
We will simplify this by changing some variables:
β = √[1–2M/R]
Since R > (9/4)M, we have 1/3 < β < 1.
r = √[R3 (1–z2) / (2M)]
z = √[1–2Mr2/R3]
Note that β ≤ z ≤ 1 < 3β.
dr/dz = –z / √[(2M) (1–z2) / R3]
dt/dz = (dr/dz) (dt/dr)
= (2√2) R √[(R–2M)/M] / ((3β–z) √[(1–z2) (z–β) (5β–z)])
So, setting aside the constants here, the integral is given by:
Integral for coordinate time, fall from R
W '(z) = 1 / ((3β–z) √[(1–z2) (z–β) (5β–z)])
W(z) = (2 (3β+1) F(φ(z) | m) – 4 Π(n; φ(z) | m)) / ((9β2–1) √[(β+1) (5β–1)])
n = (3β–1) (5β+1) / [(3β+1) (5β–1)]
m = (β–1) (5β+1) / [(β+1) (5β–1)]
φ(z) = asin(√[(5β–1) (z+1) / [(5β+1) (z–1)]])
Here F and Π are incomplete elliptic integrals of the first and third kind.
To make use of this we still need to add a suitable constant to set the origin for t, and determine the period of the motion. The two relevant locations for the particle are r = R, at the start of its descent, and r = 0, which will give us a quarter of one full period of the motion. These correspond to z = β and z = 1 respectively.
When z = β, we have:
φ(β) = asin(√[(5β–1) (β+1) / [(5β+1) (β–1)]])
= asin(√[1/m])
Using the definition of the elliptic integral F, this gives:
F(φ(β) | m) = ∫0sin(φ(β)) dt / √[(1–t2) (1–mt2)]
= ∫0√[1/m] dt / √[(1–t2) (1–mt2)]
With the change of variable t = √[1/m] u, this becomes:
F(φ(β) | m) = √[1/m] ∫01 du / √[(1–u2/m) (1–u2)]
= √[1/m] F(π/2 | 1/m)
= √[1/m] K(1/m)
Here K(m) is a complete elliptic integral of the first kind. Applying the same change of variables to the definition of the third elliptic integral yields:
Π(n; φ(β) | m) = √[1/m] Π(n/m | 1/m)
where the right-hand side has a complete elliptic integral of the third kind. We now have:
W(β) = √[1/m] (2 (3β+1) K(1/m) – 4 Π(n/m | 1/m)) / ((9β2–1) √[(β+1) (5β–1)])
So we can compute the time since the particle fell from the top of the borehole, by subtracting W(β):
tsolid, GR(r) = (2√2) R √[(R–2M)/M] (W(z(r)) – W(β))
To find the quarter-period of the borehole oscillations, we need to be able to evaluate W(z(0)) = W(1), which is a little tricky, because sin(φ(z)) has z–1 in the denominator. As z approaches 1 from below, sin(φ(z)) goes to infinity along the positive imaginary axis. So we need to evaluate the first elliptic integral F as:
F(φ(z) | m) → ∫0i ∞ dt / √[(1–t2) (1–mt2)]
A change of variable t = –i tan(u) transforms this to:
F(φ(z) | m) → i ∫0π/2 du / √[1 – (1–m) sin2 u] = i K(1–m)
For the elliptic integral of the third kind, we have:
Π(n; φ(z) | m) → ∫0i ∞ dt / ((1–nt2) √[(1–t2) (1–mt2)])
The same change of variable gives:
Π(n; φ(z) | m) → i ∫0π/2 du / ((1 + n tan2 u) √[1 – (1–m) sin2 u])
We can split this into two complete elliptic integrals:
1 / (1 + n tan2 u) = (1 – n / (1 – (1–n) sin2 u)) / (1 – n)
Π(n; φ(z) | m) → i [K(1–m) – n Π(1–n | 1–m)] / (1 – n)
This yields:
W(1) = i (2 (3β+1) K(1–m) – 4 [K(1–m) – n Π(1–n | 1–m)] / (1 – n)) / ((9β2–1) √[(β+1) (5β–1)])
The quarter-period of the borehole oscillations is then the time for the particle to fall from r = R to r = 0:
¼ Tsolid, coord(r) = (2√2) R √[(R–2M)/M] (W(1) – W(β))
We can also perform the same calculations for proper time, rather than coordinate time. In this case, we want to integrate:
dτ/dz = √[R3/(2M)] (3β–z) / √[(1–z2) (z–β) (5β–z)]
The result is:
Integral for proper time, fall from R
W '(z) = (3β–z) / √[(1–z2) (z–β) (5β–z)]
W(z) = (2 (3β–1) F(φ(z) | m) + 4 Π(n; φ(z) | m)) / √[(β+1) (5β–1)]
n = (5β+1) / (5β–1)
m = (β–1) (5β+1) / [(β+1) (5β–1)]
φ(z) = asin(√[(5β–1) (z+1) / [(5β+1) (z–1)]])
The same techniques as before let us evaluate the elliptic integrals at the endpoints of the quarter-cycle, z = β and z = 1.
We can generalise both of these calculations to the case where the object falls from rest at a different radius, and hence has a different value for E. This allows us to consider radial oscillations that take place partly in the vacuum outside the ball.
For coordinate time, we have:
dt/dz = 4 E √[R3/(2M)] / √[(1–z2) (4 E2 (3β–z)2 – (3β–z)4)]
with the integral:
Integral for coordinate time, energy E
W '(z) = E / √[(1–z2) (4 E2 (3β–z)2 – (3β–z)4)]
W(z) = (2Π(n; φ(z) | m) – F(φ(z) | m)) / √[(3β – 2E + 1) (3β + 2E – 1)]
n = –(3β – 2E – 1) / (3β + 2E – 1)
m = (3β + 2E + 1) (3β – 2E – 1) / [(3β + 2E – 1) (3β – 2E + 1)]
φ(z) = asin(√[(3β + 2E – 1) (3β – 2E – z) / [(3β – 2E – 1) (3β + 2E – z)]])
For proper time, we have:
dτ/dz = √[R3/(2M)] (3β – z) / √[–(1–z2) (3β + 2E – z) (3β – 2E – z)]
with the integral:
Integral for proper time, energy E
W '(z) = (3β – z) / √[–(1–z2) (3β + 2E – z) (3β – 2E – z)]
W(z) = 2 (2Π(n; φ(z) | m) + (3β – 1) F(φ(z) | m)) / √[(3β – 2E + 1) (3β + 2E – 1)]
n = (3β + 2E + 1) / (3β + 2E – 1)
m = (3β + 2E + 1) (3β – 2E – 1) / [(3β + 2E – 1) (3β – 2E + 1)]
φ(z) = asin(√[(3β + 2E – 1) (z + 1) / [(3β + 2E + 1) (z – 1)]])
[1] “Über das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie” [On the gravitational field of a point mass according to Einstein’s theory] by K. Schwarzschild, Sitzber. Deut. Akad. Wiss. Berlin, Kl. Math.-Phys. Tech., pp 189-196, 1916.
[2] “Über das Gravitationsfeld einer Kugel aus inkompressibler Flussigkeit nach der Einsteinschen Theorie” [On the gravitational field of a sphere of incompressible fluid according to Einstein’s theory] by K. Schwarzschild, Sitzber. Deut. Akad. Wiss. Berlin, Kl. Math.-Phys. Tech., pp 424-434, 1916.
[3] Gravitation by Charles Misner, Kip Thorne and John Wheeler, W.H. Freeman, San Francisco, 1973. Section 23.7 and Box 23.2.
|
|
|